・はじめに~具体的な数字を抽象的に表現する~
一般的に、割合やグラフを使う事で、実際にある具体的な数をわかりやすく可視的に表現することができます。しかし、初めて割合という概念を学ぶ児童の場合、ふたつの数のうちどちらが全体でどちらが部分なのかといったことはわかりづらく、身につきにくいほか、教師にとって非常に教えづらい分野でもあります。
そこで、間嶋先生の実践を紹介していきたいと思います。これを参考にして、関係図と数直線の関係についてわかりやすく説明していただければ幸いです。
・間嶋先生の指導例
1 単元名
比べて!全体と部分,部分と部分−割合とグラフ−
2 本単元で高める力
関係図と対応数直線とを合わせて使うことで数学的表現力をつける。
3 指導の構想
本単元,割合の学習は,小学校算数の中でも重要単元の一つである。
総合的な学習においても,グラフはふんだんに使われる。
さらに,グラフを除けば定着率がかなり低い単元である。私たち教師にとって,一番教えにくい単元になってしまっている。
教科書には,必ず「割合の三つの公式」が書かれている。「もとにする量」「比べる量」「割合」の三つが登場する公式である。通常,公式を丸暗記させることはしないが,割合の公式だけは例外である。少なくとも私は何の罪悪感もなく丸暗記させてきた。
円を描き,真ん中に線を引く。上に「比(べる)」という文字を入れる。下半分は,さらに縦線を入れ,「もと(にする量)」と「割合」という文字を入れる。こうやって,この三つの関係を丸暗記させて問題に応じて適用させていく。ずっと,私はこの手法をとってきた。
しかし,結果はさほどでもない。なぜだろうか。
文章問題を見たとき,どの数字がどこに入るのかが分からない。特に,「比べる量」と「もとにする量」とを明確に区別できない。与えられた問題が複雑になればなるほど,この傾向は強くなる。
公式は覚えるが,使いこなせない状態である。
こうした状態を打破するために,私は,割合の学習の際必要な,表現の使い方を教える。
その表現は関係図と対応数直線である。
本単元で獲得させたい考え方は,あるものを1とみる(百分率なら100とみる)見方である。私は,この考え方(あるものを1としてみる見方)を獲得させるとともに,本単元で,関係図と対応数直線に関わる数学的表現力を高める。
志水廣氏は言う。
割合を表現する図が必要である。私の指導経験によれば,関係図が有効であった。関係図は,割合を表すには都合のよい図である。
ただし,量感を大切にするために線分図との併用を勧めたい。
「割合の指導はそんなに難しくない」『算数教育』(明治図書1996)№489,P14
志水氏の言う「線分図」は、私が主張する「対応数直線」とはその性格が異なる。
私は,後者の方がより量感を大切にできると考えている。関係図と対応数直線とを合わせて使うことは割合の理解の上でも有効である。なぜならば,関係図によって「もとにする量」と「比べる量」との関係が分かり,対応数直線によって,二つの量の大小関係が分かるからである。
割合には,一般的に第一用法から第三用法までがある。例えば,クラブの希望者と定員,そして割合とを関係図で表すと,次のようになる。

本単元では、ある量を1とみる見方を最初に指導する。
その後,上記の第一用法から第三用法までを順序よく取り上げ,第一用法,第二用法で提案する働き掛けAからEまでを行う。
そして、第三用法とその後の「◇%引きの問題」とを取り上げ,確かに関係図と対応数直線とを合わせて使うことができるかを確かめる。最後に,グラフを身近な素材とともに扱う。
課題提示後,数学的表現力を高めるために,以下の働き掛けを行う。

「細分化」とは,図や表と言葉・式とを分けたり,言葉・式を考えの順序に沿って三つに分けたりすることである。自分の考えを細かく丁寧にかかせることによって,図や表は課題の全体的な構造をとらえるのに役立つ。一方,言葉・式は筋道を立てて考えるのに役立つ。細分化してかかせることによって自分が使うことのできる数学的表現を自覚させることができる。

まず,二つの表現を提示する。一つは関係図と数直線が描かれている表現である。もう一つは対応数直線と若干の説明がかかれている表現である。なお,関係図は全くの未習であるため、これは教師側から提示する。
次に,これら二つに共通していることを問う。これによって子どもは,表現の使い方の違いを意識する。このとき,思考するスキル「関連付けて考える」を使わせる。Aの表現とBの表現を関連付け,共通点を探すのである。
最後に,どちらが考えを分かりやすく表しているかを選ばせ,その理由も問う。これによって,関係図と対応数直線のよりよい使い方が様々挙がる。このとき,思考するスキル「複数の観点から考える」を使わせる。例えば,「関係図があると,二つの量の関係が分かって、より分かりやすくなる。」とか,「対応数直線があると,答えがおよそどのくらいか見当が付く。」などと思考する。端的に言えば,これによって,関係図と対応数直線のよさが抽出されるのである。

様々に挙がった関係図や対応数直線のよりよい使い方の中から,自分にとって必要な使い方を選ばせる。これによって,子どもは働き掛けAで表現した考えを見直し,「これでよいか。」「よりよくよく伝わるには,どういう使い方が不足しているのか」を自覚する。

自分に不足している使い方を自覚した子どもは,自分の表現を修正し,よりよい使い方をした表現に修正することができる。

相手の数学的表現の変容を評価する。評価の際は,相手が選んだ「よりよい使い方」に照らして,実際,修正されているのかどうかを評価させる。よりよい使い方ができているときは,よい評価を相手からもらう。そのため,成就感や満足感をもつことが出来る。
また,相互評価活動の中で,自分にもなく全体の場でも出されていない数学的表現のよりよい使い方があることに気付き,そのよさを感得する。例えば,「面積図で,もとにする量と比べる量とを表すことによって,大小関係がすぐに分かる。」といったことである。
4 本時の構想 (6~9Q/36Q)
(1) 主眼
割合を求める問題を解決する方法を二つの表現で比較検討することを通して,関係図と対応数直線の表現のよさを知り,それを生かして自分の表現を修正できるようにする。
(2) 展開
学習活動と子どもの意識・思考
教師の働き掛け



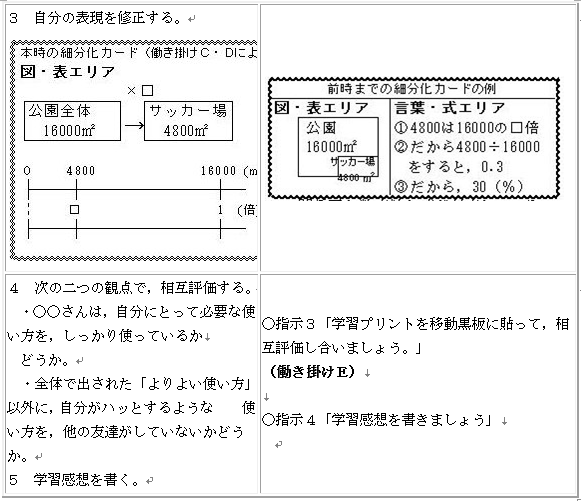
(3) 評価
- 働き掛けAとBによって,関係図と対応数直線のよりよい使い方が分かる。具体的には,働き掛けCの後,自分の表現に不足している使い方を板書された使い方の中から取り出すことができる。
- 働き掛けCとDによって,関係図と対応数直線のよりよい使い方ができる。具体的には,働き掛けDの後,取り出した使い方を使って,修正できている。
- 働き掛けEの相互評価によって,関係図と対応数直線のよりよい使い方をすると,誰もが納得できる表現になると感じたり,相手の数学的表現を見て,自分にはない数学的表現のよりよい使い方があることに気付き,そのよさを感得したりする。具体的には,学習感想と,相手への評価の言葉から検証する。
・編集後記
自分自身も小学生の時、割合やグラフの問題では、特に文章題で、どちらが割る数でどちらが割られる数なのかといったことがわからなかったり、「全体というのはどこ…?」といった状態になったりしてなかなか理解できなかったこともありました。
しかし、この実践を使えば、覚えてあてはめるという以外の方法でこの難しい単元を理解させるに導くことが出来るのではないかと思いました。
(編集・文責:EDUPEDIA編集部 佐藤 直輝)
<実践者プロフィール>
間嶋 哲(Mazima Akira)
1965年、新潟県に生まれる。新潟大学教育学部を卒業。
新潟県内の小学校で活躍後、文部科学省での1年間の研修を経て、現在、新潟市教育委員会学校支援指導主事。算数授業ICT研究会理事。全国算数授業研究会総務幹事。
趣味は、海外旅行・外国語会話・スキー・ギター(フォークとクラシック)・読書・園芸・熱帯魚飼育など、多岐に渡る。
大学の卒業旅行を機に、旅行・外国語にはまり、旅行記を一冊出版したほどのエピソードを持つ。
- HP
間嶋哲のHPへようこそ… http://bit.ly/homepage_majima



コメント