1 概要
この実践記事では、小数の掛け算を既習の知識を用いながら学習します。そして、子ども同士のコミュニケーションを通して数式の理解力を養い、数学的表現力を高める実践です。
2 単元名
小数をかける計算
3 本単元で高める力
数学的表現力を高める。本単元で獲得させたい知識・技能は、2本の数直線を使って、小数をかける計算の仕方を既習の計算方法に直すことである。
数学的表現力が高まった状態を、次の3つの状態で表す。
【内容知(分かる)】小数をかける計算の仕方を表現する際、2本の数直線の使い方が分かる。
【方法知(できる)】小数をかける計算の仕方を2本の数直線を使って表現することができる。
【体験知(実感する)】小数をかける筆算の仕方のよさを実感する。
なお,実感させるために必要なその子なりのこつは、小数をかける筆算の仕方を考える際に使う、自分にとって使いやすい表現の仕方である。
4 指導の構想
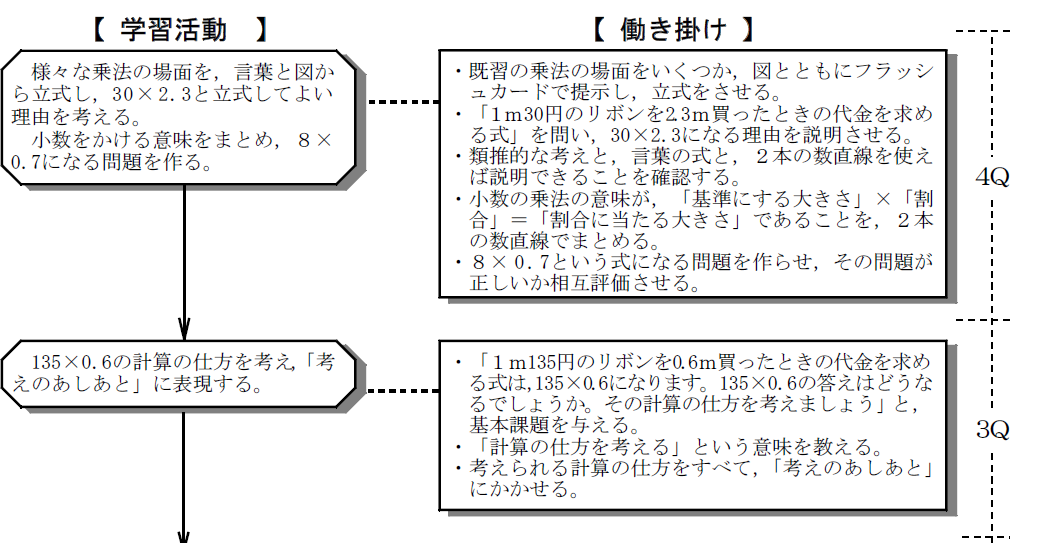
既習の乗法の場面をフラッシュカードで提示し、それぞれを立式させる。その後、本単元で扱う「×小数」の場面を提示し立式させる。そして、「×小数」と立式できる理由を考えさせる。
こうして、小数をかける計算の意味を拡張(「基準にする大きさ」×「割合」=「割合に当たる大きさ」)させる。その際、主な理由として、類推的な考え、言葉の式、2本の数直線を扱う。
その後、次の基本課題を与える。
1m135円のリボンを0.6m買ったときの代金を求める式は、135×0.6になります。135×0.6の答えはどうなるでしょうか。その計算の仕方を考えましょう。
その際、「計算の仕方を考えること」とは「単に筆算の仕方を答えることではなく、答えを求めるために、習ったことをどのように使えばよいのかを考えること」と説明する。そして、考えられる計算の仕方をすべて、『考えのあしあと』にかかせる。
その後、次の働き掛けを行う。
<働き掛け1> 2本の数直線を使って計算の仕方を説明している表現を2つ提示し、説明させる。
提示する2つの表現は、次の表現である。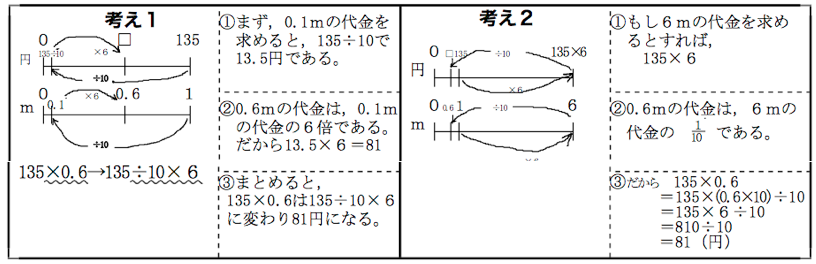
このことによって、子どもは、上の2つの表現をした子どもや、2つの考え方に気付いた子どもの説明を注意深く聞き、2つの表現にある考え方を知ろうとする。
その後、次の働き掛けを行う。
<働き掛け2> 提示された表現を使って、グループで説明し合わせる。
このことによって、子どもは2つの表現を使えば、既習のわり算やかけ算を活用して、計算の仕方を表すことができることを知る。ここで、子どもは、技能スキル「図や具体物を使う」を使って、図エリアにある2本の数直線を使いながら説明をする。
グループの中では、説明ができそうな子どもから説明をさせる。初めは説明ができないと思っていた子どもも、説明を何度か繰り返し行わせることによって、これら2つの表現にある考え方が、次の2つであることに気付く。
○ 0.1mの代金を135÷10で求め、その後、6倍する。式にすると、135÷10×6。
○ 6mの代金を135×6で求め、その後、10でわる。式にすると、135×6÷10。
その後、次の働き掛けを行う。
<働き掛け3> 提示された表現の工夫を話し合わせ、取り入れたい表現の仕方を問う。
このことによって、子どもは、気付いた考え方の基になる表現の仕方に着目する。そして「何があるから、その考えが分かるのか」と考えるようになる。ここで、子どもは、話すスキル「自分の意図がよく伝わるように話す」を使って、友達の意見を引用したりまとめたりする。
子どもが挙げる表現の工夫を、表現の仕方として短くまとめる。

これらの表現の仕方を短冊カードに書く。その後、働き掛け1以前にかかせた表現を振り返らせ、取り入れたい表現の仕方を問う。すると、子どもは2本の数直線に関わる表現の仕方(aやk)を挙げる。直す必要があるときは、かいた表現を赤ペンで修正させたり、新たにかき直させたりする。
こうして、子どもは、小数をかける計算の仕方を表現する際、2本の数直線の使い方が分かる。
その後、次の類似課題を与える。
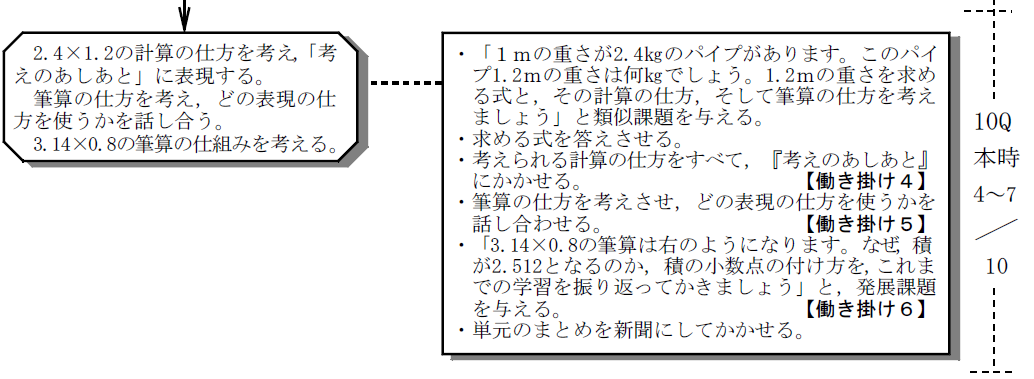
@<color>{#0000ff,1mの重さが2.4㎏のパイプがあります。このパイプ1.2mの重さは何㎏でしょう。1.2mの重さを求める式と、その計算の仕方を考えましょう。
}
式については、全員で確認する。そして、次の働き掛けを行う。
<働き掛け4> 考えられる計算の仕方を『考えのあしあと』にかかせる。
このことによって、子どもは、2.4×1.2の計算の仕方を考えようとする。ここで、子どもは、思考するスキル「既習事項を想起する」を使い、取り入れたい表現の仕方を使って解決する。
こうして、子どもは、小数をかける計算の仕方を2本の数直線を使って表現することができる。
その後、次の働き掛けを行う。
<働き掛け5> 筆算の仕方を考えさせ、どの表現の仕方を使うかを話し合わせる。
このことによって、子どもは,2.4×1.2の筆算の仕方を、『考えのあしあと』を見ながら考える。そして、積が2.88となることから、積の小数点の打ち方に着目する。
その後、積の小数点の打ち方と、表現の仕方とが、どう関連付くのかを話し合わせる。ここで子どもは、話すスキル「自分の意図がよく伝わるように話す」を使い、選んだ表現の仕方がどこに使われているのかを示しながら発言する。
そして、その子によって、使う表現の仕方が違うことに気付く。こうして、友達の意見を聞きながら、自分なら、どの表現の仕方を使えるかを考える。
その後、次の発展課題を与える。
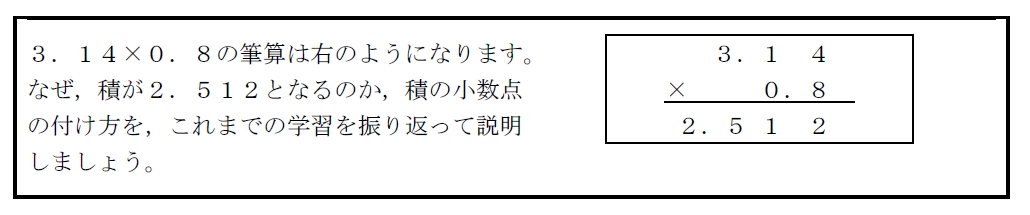
<働き掛け6> 使いたい表現の仕方を選ばせ、積が2.512となる理由をかかせる。
このことによって、子どもは、選んだ表現の仕方を使って解決する。ここで、子どもは、思考するスキル「既習事項を想起する」を使い、2.4×1.2の筆算の仕方を話し合ったことを想起し,
3.14×0.8の筆算の仕方をかく。
こうして、子どもは、算数表現のこつを自覚して使い、発展課題を解決することができるからこそ、数学的な考え方と表現の仕方とを関連付け、「積の小数部分のけた数は、被乗数と乗数の小数部分のけた数の和にする」筆算の仕方のよさを実感する。
5 指導計画全27Q <9時間>
6 本時の構想(21Q~24Q/27Q)
(1)主眼
2.4×1.2の筆算の仕方を説明する際、どの表現の仕方を使うか話し合うことを通して、その子なりの表現のコツを考えさせ、筆算の仕方のよさを実感させるようにする。
(2)主張
このような子どもにC0
○ 次のどちらかのことが分かっている。
- 2本の数直線を使って,乗数の0.1当たりの量を求めれば、小数をかける計算の仕方を説明できることが分かる。
- 2本の数直線を使って、乗数の10倍当たりの量を求めれば、小数をかける計算の仕方を説明できることが分かる。
○ 次のことができている。
- 2.4×1.2の計算の仕方を『考えのあしあと』にかいている。
このように働き掛けると(働き掛け5)※上記参照
- 黒板に2.4×1.2の筆算(式だけ)をかく。
指示「2.4×1.2の筆算の仕方を考え、ノートにかきましょう。」
- その後、発表させる。
発問「積の小数点が、このように付くのはなぜですか。それを説明するのに必要な表現の仕方はどれですか。」
指示「必要な表現の仕方をいくつか選んで、積の小数点が、このように付く理由を説明しましょう。」
- 様々な理由を説明させる。
補助発問「□□の表現の仕方を使って説明することはできませんか。」
※□□には、『仮定の言葉』『整数の式にしている』『2本の数直線に式や矢印が入る』が入る。
このような活動・思考が促されC1
○ 自分の「考えのあしあと」を見ながら、筆算の仕方を考え、ノートにかく。
○ 積の小数点が2と8の間に付く理由を考え、説明するのに必要な表現の仕方をいくつか選び、説明する。
- 説明に必要な表現の仕方は、『仮定の言葉』です。積の小数点がこのようになるのは、2.4×12をすると28.8になる。でも、それは、もしかける数が12だったらということです。本当は、かける数が1.2なので、出た答えを10でわらないといけません。だから、28.8の小数点が左に一つ進んで、2.88になります。
- 説明に必要な表現の仕方は、『整数の式にしている』です。積の小数点がこのようになるのは、2.4×1.2を24×12に変えて計算しているからです。小数×小数を整数×整数にしています。2.4を10倍して24、1.2を10倍して12としたのだから、出た答えを100でわらないといけません。だから,24×12の答え288が2.88に変わります。
- 説明に必要な表現の仕方は、『2本の数直線に式や矢印が入る』です。図で説明するとこうなります。(2本の数直線で説明する)
○ 友達の意見を聞きながら、自分ならば、どのように説明することができそうか、使う表現の仕方は何かを考える。
※ ここで、子どもは話すスキル「自分の意図がよく伝わるように話す」を使う。取り出した表現の仕方がどこに使われているのかを示しながら発言していたら、このスキルを使っていたと判断する。

指示「使いたい表現の仕方を選んでプリントの上の四角にかきましょう。そして、実際にプリントの下の四角に、積が2.512となる理由をかきましょう。」
このような活動・思考が促されC2
○ 自分が使いたい表現の仕方を選ぶ。
○ 算数表現のこつを使って、積の小数点が2と5の間に付く理由をかく。
- 積の小数点が2と5の間に付くのは、3.14×8をすると25.12になります。でも、実際は、もしかける数が8ならば…ということです。本当は、かける数が0.8なので、出た答えを1/10にしなければいけません。(説明に必要な表現の仕方は,『仮定の言葉』)
- 積の小数点がこうなるのは、3.14×0.8を314×8に変えて計算しているからです。3.14を100倍して314、0.8を10倍して8にして計算したのだから、出た答えを1000でわらないといけません。だから、2512ではなく、2.512になります。(説明に必要な表現の仕方は、『整数の式にしている』)
- 2本の数直線でも説明できます。(実際にかく)(説明に必要な表現の仕方は、『2本の数直線に式や矢印が入る』)
※ ここで、子どもは思考するスキル「既習事項を想起する」を使う。2.4×1.2の筆算の仕方を話し合っていた際に説明された表現の仕方が使われていたら、このスキルを使っていたと判断する。
このように働き掛けると
指示「発展課題が終わった人は、授業追想記をかきましょう。」
- 発展課題が終わっていない子どもも、授業終了5分前には、追想記をかかせる。
このようになるCn
○ 小数をかける筆算の仕方のよさを実感する。
- 「小数のかけ算では,小数点の動かし方に仕組みがあることが分かった。例えば、『整数の式にしている』を使うと、2.4×1.2が24×12と変身できることが分かる。」
- 「小数×小数では、小数点の位置が、かける小数とかけられる小数分だけ動く。なぜそう動くかというと、2.4×1.2なら2.4×12に直すことができるからだ。これは、『かける数の10倍当たりを求める』を使っている。2.4×12の答え28.8を10でわると、2.88になる。
7 検証
(1)検証すること
- 働き掛け5(小数の筆算のやり方を子ども達同士で意見を交換する)が、その子なりのこつを獲得させるのに有効に働くかどうかを検証する。
- 働き掛け5と6(筆算のやり方を既習事項から導く)が、小数をかける筆算の仕方のよさを実感するのに有効に働くかどうかを検証する。
(2)対象と方法
小数をかける計算の仕方を表現する際、2本の数直線の使い方が分かり、小数をかける。
計算の仕方を2本の数直線を使って表現することができた子ども5名を対象とする。
〔その子なりのこつ〕
働き掛け6でかかせるプリントを見て、次の2つのことが確認できた場合、働き掛け5がその子なりのこつを獲得させるのに有効であったと判断する。
- 自分が使いたい表現の仕方を選んでいる。(いくつ選んでもよい。)
- その表現の仕方をすべて使って、積の小数点が2と5の間に付く理由を正しく書いている。
〔実感〕
授業終わりに書かせる「授業追想記」から判断する。Cnで想定したように、小数点の付け方と表現の仕方とを関連付けている記述があれば、働き掛け5と6が,小数をかける筆算の仕方のよさを実感するのに有効であったと判断する。
8 編集後記
近年理数離れが進んでおり、子どもたちは実際の理系の職には勉強が関係ないと思っているようです。しかし、間嶋先生の算数の実践は自主的に、論理的に学んでいけるような姿勢を形作る実践になっています。子どものやる気も湧きますし、将来に役立つスキルも身につけられる素晴らしい実践です。
(編集・文責:EDUPEDIA編集部 坂本一途)
9 <講師プロフィール>
間嶋 哲(Mazima Akira)
1965年、新潟県に生まれる。新潟大学教育学部を卒業。
新潟県内の小学校で活躍後、文部科学省での1年間の研修を経て、現在、新潟市教育委員会学校支援指導主事。算数授業ICT研究会理事。全国算数授業研究会総務幹事
趣味は、海外旅行・外国語会話・スキー・ギター(フォークとクラシック)・読書・園芸・熱帯魚飼育など、多岐に渡る。
大学の卒業旅行を機に、旅行・外国語にはまり、旅行記を一冊出版したほどのエピソードを持つ。
●HP
間嶋哲のHPへようこそ… http://bit.ly/LzzKmJ







コメント