1.1 はじめに
今回紹介するのは、5円切手と6円切手を組み合わせてできる数(和)を、算数的活動を通じて学ぶというものである。これは関数的な考え方にも通ずる。
関数的なものの見方というのは、算数・数学の教育の中で、昔から大切であると言われてきた。ただ、その考え方をきちんと理解している生徒は高校生でも少ない。このような現状の中、小学生のうちに少しでも関数的な考え方に触れさせることに大きな意味があるので、これから紹介する間嶋先生の実践をぜひ参考にしてほしい。
1.2 間嶋哲先生による授業例
(引用元: http://bit.ly/Rjvtc7)
単元名
5円切手・6円切手
めざす子どもにするための方策
4年生に『ともなって変わる量』の単元がある。関数的なものの見方を育てるうえで,重要な単元の一つである。そこでは,二つの量を設定し,ある量が増えたらどうなるのかという視点で考えさせる。算数の世界には,完全に関数的な対応でなくとも,ある一定のきまりが自然に生まれてくる場合がある。今回の題材も,そのような題材である。
5円切手と6円切手の何枚かの組み合わせによって,どんな金額が表せるかを考えさせる。「公倍数」あたりが関係しそうであるが,実は全く関係ない。例えば,「30円」は,5円切手が6枚,あるいは6円切手が5枚で表せる。当然,「5円」「6円」も表せる。それでは,「7円」と言われると,もう無理である。「8円」も「9円」も同様である。
「10円」は5円切手2枚で,「11円」は5円切手と6円切手が1枚ずつで表せる。たっぷりと活動させた後で,「表せない金額」の最高値を問う。
その数は,意外と小さな数である。
そして,そこには,見つけるための,あるきまりが存在する。
しかし,一般には,そのきまりに気づきにくい。そこで,三つの手だてを行う。
手だての一つめは,自分で考えた「表せる金額」を大判の座席表に書かせることである。このことによって,「あっ,その金額は表すことができるのか」という友達の気付きを共有することができる。自分ではきっとできないと思っている金額でも,組み合わせによってできることが分かれば,自分の思考をさらに研ぎ澄ます姿勢が生まれる。
手だての二つめは,自分たちで「表せる金額」の結果をどんどん板書で整理し,その並び方によって,下記のように,何かしらのきまりを発見しやすいようにすることである。ちなみに,表せる数を太字にすると,そこから見えるきまりは,一目瞭然である。「表せない金額」の最高値は「19円」である。
1 2 3 4 5 6
7 8 9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29
手だての三つめは,「表せない金額」の最高値が,もしかすると「29円」よりもっと大きな数であるかもしれないと,ゆさぶることである。
こうした活動の後 最後に,6円切手を4円切手に変え,4円切手と5円切手ならばどうなるのかを問う。同じように並べて記入することで,実は同じようなきまりが存在することに気付かせたい。このことは「それなら,6円切手と7円切手なら,どうなるのかな」という発展的な思考を生むにちがいない。
単元の目標
2種類の切手を組み合わせ,「表せない金額」の最高値を考えることを通して,そこにあるきまりを見つけたり,発展的に考えたりすることができる。
指導計画(2時間扱い)
第一次 5円切手6円切手…………………2時間(本時は1/2)
本単元は,単元『ともなって変わる量』の発展的な扱いとする。
本時の指導
目標
5円切手と6円切手を組み合わせることで,できる金額とできない金額を考え,きまりを見つけたり,発展的に考えたりすることができる。
展開
主な学習活動
- 5円切手と6円切手を組み合わせて様々な金額を表す。
- 5円切手と6円切手だけでは表せない金額を考える。
- なぜ「19円」が,5円切手と6円切手だけでは表せない最高値なのか話し合う。
- 切手の種類を変えて,発展的に考える。
指導上の留意点
- 5円切手と6円切手を何枚か組み合わせて,いくらになるのか考えさせる。
- 自分で考えた「表せる金額」を,大判の座席表に様々書かせる。
- 例えば,16円=5円×2+6円×1のように,式で表現させる。
- 「表せる金額」を整理して板書する。
- 5円切手と6円切手の組み合わせでは表せない金額を問う。
- 「表せない金額」の最高値を考えさせる。
- 4円切手と5円切手ならば,どうなるのかを問う。
1.3 編集後記
5円切手と6円切手を実際にたくさん使って組み合わせて考えさせるという、算数的活動を児童に行わせる面白い教材だと思った。このような活動は児童が自然と楽しめる。
また、今回の授業の中で、非常に面白いと思ったのは実際に5円切手と6円切手以外の切手での組み合わせではどうなるのかということを考えさせることだ。一つの問題を理解したあと、似た問題を自分で考えるということの中で、問題の本質に気づくことができるからだ。
(編集・文責:EDUPEDIA編集部 宮崎雅人)
1.4 <講師プロフィール>
間嶋 哲(Mazima Akira)
1965年、新潟県に生まれる。新潟大学教育学部を卒業。
新潟県内の小学校で活躍後、文部科学省での1年間の研修を経て、現在、新潟市教育委員会学校支援指導主事。算数授業ICT研究会理事。全国算数授業研究会総務幹事
趣味は、海外旅行・外国語会話・スキー・ギター(フォークとクラシック)・読書・園芸・熱帯魚飼育など、多岐に渡る。大学の卒業旅行を機に、旅行・外国語にはまり、旅行記を一冊出版したほどのエピソードを持つ。
●HP
間嶋哲のHPへようこそ… http://bit.ly/homepage_majima





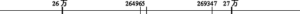
コメント