1 間嶋哲先生の授業例
1.単元名
2けたでわるわり算
記事の引用元
- 間嶋哲先生の授業例 http://p.tl/qnlB (第4学年 算数1組 算数科学習指導案)
- 児童の反応 http://p.tl/WCip (9月の新津第一小学校 少人数・算数指導 日記)
2.単元の目標
除数が2けたの場合について,被除数がどんなに桁数の多い大きな数になっても同じ手順の繰り返しで計算できることを知り,正しく計算できることから,手順のよさを感じ取ることができる。
3.単元の評価規準
【A「数と計算」 】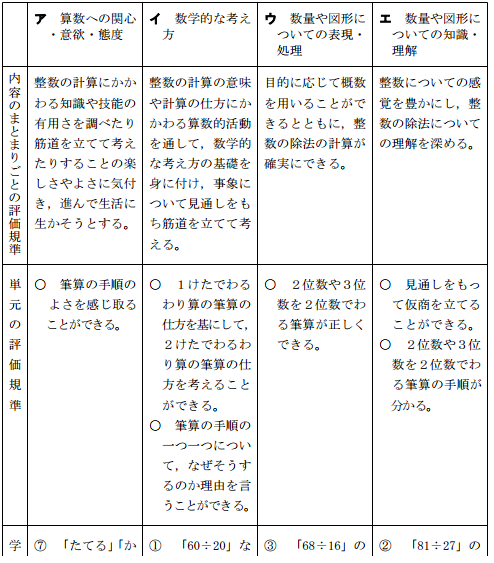

4.指導と評価の計画





5.各時間における観点別評価と,その総括の仕方
授業の毎時間,4観点にわたる評価を行うことは不可能である。そこで,各時間のねらいに照らし合わせ,1~2観点を重点的に評価する観点として設定する。それを「指導と評価の計画」の中で,○印で示した。
一般的に本単元は 「数と計算」領域の中でも,「表現・処理」の観点が重視される単元である。しかし 「表現・処理」の前提にあるのは 「仮商を正しく素早く見付ける」力であり,これは「知識・理解」の観点に含まれる。また,生きた知識として今後に活用されていくには 「なぜ,その手順で筆算をするのか」を考えさせたり,説明させたり,新たな問題に意欲をもって取り組ませたりすることが重要である。これは 「数学的な考え方」や「関心・意欲・態度」に含まれる。
本単元の授業ごとに,各個人の評価の記録をとっていく。十分満足できる状況と判断されるときはA,おおむね満足できる状況と判断されるときはB,努力を要する状況と判断できるときはCとして記録しておく。
そして,単元全体を通して,それぞれの観点について,Aが過半数以上の個数であれば,その単元における観点別評価は,十分満足できる状況と評価する。また,それぞれの観点についてCが過半数以上の個数であれば,努力を要する状況と判断する。どちらにも該当しない場合は,おおむね満足できる状況と総括する。
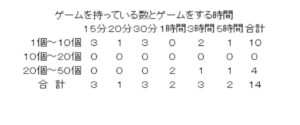
例えば,本単元の各時間において,ある児童の評価の記録が以下のようであったとすると,本単元における観点別評価の総括は,表の最下段のようになる。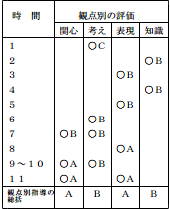
6.本単元におけるA学力(基礎学力)・B学力(基礎・基本)
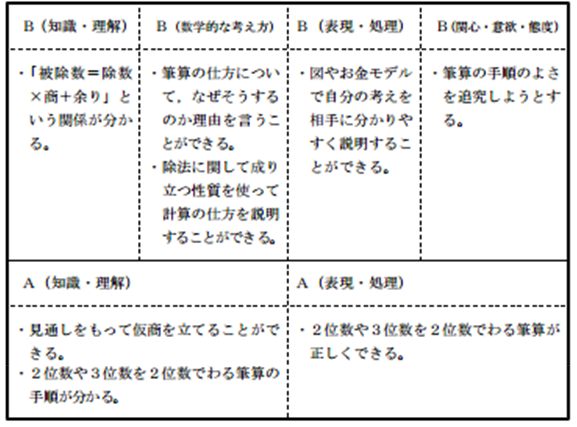
7.系統図
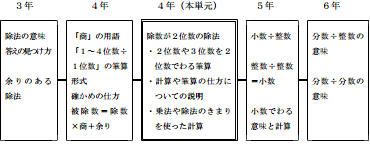
8.指導の構想
(1)単元について
1学期に「わり算 」「1けたでわるわり算」2つの単元で,わり算の筆算の仕方を学習している。ここでは,除数が2けた(2位数)になった場合の筆算の仕方を学習することが中心である。
この学習で最も大切なことは「仮商を正しく素早く見付ける」力を付けることである。その力がないと、どの数字がたつのかを考えて筆算が進まなかったり、仮商はたてたが過大商になったり過小商になったりして何度も消しゴムを使う状況が生まれる。これでは「除法の計算が確実にできる(指導要領の記述より)」ことに結び付かない。
(2)児童の実態
「わり算」「1けたでわるわり算」の単元では,お金モデルを基にして筆算の仕方を説明させる活動を中心に行った。そして 「たてる」「かける」「ひく」「おろす」という筆算の手順を繰り返し指導した。その結果,1学期に行った全校計算テスト(問題の全てが,わり算の筆算)では数名を除き,9割を超える正解率に達した。
習熟度別クラス編成をしているものの,本「算数1組」(編注:間嶋先生が担当した学級)は,新たな学習課題に対して既習事項と結び付けて様々なアイディアを表出していくことが苦手である。また,アイディアがあっても,それを分かりやすく伝えていくこともまだ十分とはいえない。
そこで,じっくりと学習課題に向かわせたり,継続して一貫した指導を試みたり,面白いアイディアに出会わせたりすることが必要である。
(3)指導の重点
「仮商を正しく素早く見付ける」力を付けるために,次の2つを指導の重点として設定する。
① 仮商の修正をしなくてもよい筆算の仕方を図と対応させながら教え,習熟させた後,通常の筆算の仕方と比較させる。
② 毎時間,2位数×1位数の暗算練習をさせる。
<①について>
子どもにとって,本単元の学習はどうしても機械的な操作だけで終わりがちである。それ自体が無味乾燥な作業で終わることで,筆算の手順のよさを感じ取ることができなくなる。また,それ以前に,計算結果の見通しを立てて「仮商を正しく素早く見付ける」力も付かない。 そこで左下の筆算の仕方を教える。参考として通常の筆算の仕方を右下に載せる。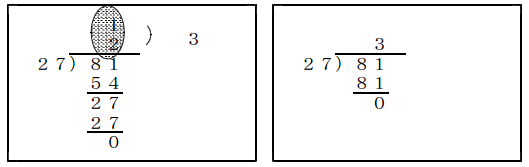
通常の筆算の仕方と比べると,やや遠回りの印象があるが,実はこの筆算の仕方は「仮商の修正をしなくてもよい筆算の仕方」なのである。さらに付け加えると「何の数字が立つのかな」と考えずに済む方法でもある。
もちろん最終的には,左上の筆算の仕方が右上の筆算の仕方になっていくことが望ましい。左上図○の部分がどれくらい短くなっていくのかが,実は子どもの「仮商を正しく素早く見付ける」力の高まりに他ならない。
<②について>
本単元を指導するに当たり これまでの学習で身に付けさせたい「基礎学力」は、「2位数×1位数の暗算」である。例えば「96÷33」というわり算を考えたとき「33×3」が素早く暗算できたなら 「3をとりあえずたてる」現象は生まれない。
9.本時の指導 (7/11)
(1)本時の目標
○ 「たてる」「かける」「ひく」「おろす」の4つの手順が繰り返される,除法における筆算の手順のよさを感じ取ることができる。【関心・意欲・態度】
○ 2つの筆算の仕方を比較検討する活動をとおして,共通点や相違点に気付くことができる。【数学的な考え方】
(2)展開
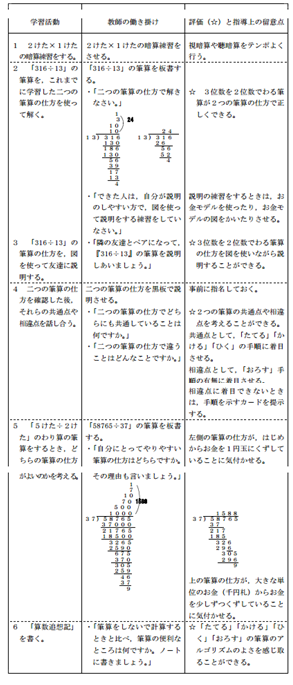
2 児童の反応
引用元は間嶋先生ホームページ( http://p.tl/WCip)原文のまま
授業感想
- 少しずつの計算は1こ数をたてていくからたくさんになるけど計算はバッチリで,パッとの方はすぐできてやりやすい。(T)
- ズバッと計算がやりやすい。なぜなら何÷何と考えると,頭の中でこのぐらいの答えだなと分かるからズバッと計算の方がやりやすい。(N)
- パッとする筆算の方がやりやすい。少しずつだと,何回も何回もしなければいけないから。少しずつの方が確実だけど,パッとの方がやりやすい。難しいのは少しずつの方。何回もするから,途中で筆算が間違っていると全部だめになる。(T)
単元をとおしての感想
◎ズバット計算と少しずつ計算があって,とても楽しかったです。ぼくは,ズバット計算の方が得意でした。ぼくは暗算が得意なので,やりやすい!と思いました。これからもがんばろうと思います。(Y)
◎ズバット計算のときは,1,2,3をたてないで10をたてると,やりやすくなることが分かった。(T)
◎2けた÷2けたのわり算の筆算は,3けた,4けた,5けたのわり算の筆算と同じやり方でやれば簡単だったから,楽しかったし,6けたもやりたかったです。(K)
◎2けたでわるわり算は,1けたでわるわり算より難しかったけど楽しかった。やり方が同じだからだ。(K)
◎2けたでわるわり算は,2けただから難しいと思っていたけど,本当は1けたと同じということが分かって,よかったと思います。(Y)
◎少しずつやる筆算は,何回もたてたりかけたりひいたりするのがあって楽しい。(N)
編集者補足
児童の感想中での『少しずつ計算』『少しずつの計算』は下図(再掲)の左、『ズバッと計算』『ズバット計算』『パッとする筆算』は下図の右のことだと思われます。
3 編集後記
少しずつ筆算は、仮商を正確に考える必要がないため、筆算に対する苦手意識を持たせない指導法としては優れていると感じました。ただ、通常の筆算の方法を習熟させるためには暗算力が必要なので、それを養うための施策も日常的に行う必要があると考えます。
授業の感想にあるように、児童が算数への楽しさを感じられるようになれば素晴らしいと思います。
(編集・文責:EDUPEDIA編集部 西島宗直)
4 実践者プロフィール
間嶋 哲(Mazima Akira)
1965年、新潟県に生まれる。新潟大学教育学部を卒業。
新潟県内の小学校で活躍後、文部科学省での1年間の研修を経て、現在、新潟市教育委員会学校支援指導主事。算数授業ICT研究会理事。全国算数授業研究会総務幹事。
趣味は、海外旅行・外国語会話・スキー・ギター(フォークとクラシック)・読書・園芸・熱帯魚飼育など、多岐に渡る。
大学の卒業旅行を機に、旅行・外国語にはまり、旅行記を一冊出版したほどのエピソードを持つ。
●HP
間嶋哲のHPへようこそ… http://p.tl/vuWm
●記事の出典
・間嶋哲先生の授業例 http://p.tl/qnlB (第4学年 算数1組 算数科学習指導案)
・児童の反応 http://p.tl/WCip (9月の新津第一小学校 少人数・算数指導 日記)





コメント