1 概要
この実践は(株)教育同人社の許可を得て、「はなまるサポート」の学習指導ポイント一覧より転載しています。
実践の続き(無料)は下部のURLからご覧ください。
また、以下より実践をPDFでダウンロードできます。
添付ファイル
2 はじめに
□が用いられる場合について
3年生では□は未知の数量を表す記号として使い、問題の示す通りに数量の関係を立式し、□にあてはまる数を調べることができるようにします。つまり、□を「数をかく場所」として扱うのです。そして次第に未知の数量を表す記号として使えるようにして、5年生の「文字と式」で□のかわりにa、b、xなどを使うように指導していきます。
□+6=15、□−8=7、15−□=6、□×5=30、□÷7=8などのように、問題に示されている順序に従って立式することのよさを味わわせるようにします。そして□は、おおよそその立式の逆算で求められることを知ることになります。
3 □を使った指導例②
逆思考の問題を扱う方法(八木 隆先生のアイディア)
①2年生で学習した以下のような問題を提示する。

この問題を解くのに、子どもたちは「なに算になりますか?」の問いに対して、「たし算」「ひき算」の両方を答えることが多いのです。
●「たしざん」と答える理由
- 6人乗ってきたから,前より6人増えている。だから「増えるたし算」です。
- 「全部で」と言っているのだからたし算です。
●「ひきざん」と答える理由
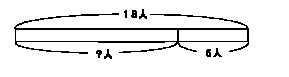
テープ図にかいてみると,上図のようになり,わからないところを求めるのだから、18−6になります。
このようなことから、テープ図に表すと答えを求めるのになに算か分かりやすいこと、「「たし算」に見えても、答えは逆の「ひき算」で求められるものがあることなどを指導するのです。従ってこの問題は既習事項です。ですから、ほとんどの子どもたちが、答えを求める式、18−6と立式するでしょう。
これは2年生での学習がよく理解されていたことを示すものです。
②本当に「18−6」の式でよいかを確かめるため、「18−6」の式になる問題を作る
- 「18人いて6人へりました。残りは何人でしょう。」
- 「男子18人と女子6人の違いは何人でしょう。」
このような問題を作ります。これは、一番最初に示した問題とは違うものです。
問題がこのように違うのに、どうして18−6でいいのですか?と再度問います。すると子どもは、「はじめにいた人を出すのだから、もともとたし算なんだけれど、答えを出すのには18−6のようにひき算をする」ことに気づきます。
そこで、それでは「もともとのたし算」ってどんな式ですか?と問います。
子ども:何人かに6をたすたし算です。
子ども:?+6です。
このたし算の答えはわからないですか。
子ども:答えは18です。
子ども: ?+6=18の式です。
分からないところを□にすると,□を使った式で □+6=18 と書けます。
と教師から教えます。
③□+6=18の求め方を考える。


テープ図から、□=18−6
このように、□を使った式から□を求める方法はいくつかありますが、最も簡単・簡潔・明瞭な方法はどれか考えさせます。そして逆算の考え方やテープ図、線分図による数の関係をみて決める方法を強調します。
注意すること
教科書でも「四則計算相互の関係から逆算で求める方法」をまとめています。その場合、「たし算→ひき算で ひき算→たし算で」のように解釈されがちですが、例えば12−□=7のような場合は、□はひき算で求めることになります。かけ算と割り算の場合も同じように注意する必要がある場面があります。
4 指導上の留意点
この展開例では、「既習事項を使って解決する」ことと、そのことから発生する課題を解決するという問題解決の手法です。
新しい指導要領の実施に伴い、各教科書はテープ図の扱い方を従来とは大きく変えました。それは、これまで「逆思考」の問題場面で数量の関係を整理する必要性からテープ図を導入してきた流れを、「順思考」の問題場面から適用し、数量の関係を明確に表す方法として早期から指導している点です。
従って、3年生のこの時期は、テープ図で数の関係を表すことが十分できることが前提の指導展開が考えられます。
子どもたちは2年生で、逆思考の問題は既に経験しています。またその答えを求める場合には、テープ図で数量の関係を明らかにして、何を求めるのか、そのためにはなに算をすればよいのか理解しています。
しかし、逆思考の問題では、「本当はたし算なのに、答えはひき算で求めるのだ。」と考え、「増えた」「全部で」「減った」「残った」など、しばしば問題に出てくるキーワードや動作からイメージする演算決定の方法があてにならないのかなと思ってしまっているのです。その問題をすっきりさせ、□を使って順思考で表すという算数のよさを味わわせるのが目的です。「18−6」の問題作りがやや唐突な感じもしますが意図を理解していけば可能な指導でしょう。
5 実践者紹介
山﨑 憲
元東京都算数教育研究会会長。
「小学校時代から現在までで,今が最も算数がすき」と,小学校退職後も算数教育に没頭し,現職時代に引き続き年に数回研究授業も試みている。
現在東京学芸大学講師として初等算数科教育法を担当。
またボランティアとして東村山市算数教室を開催し算数好きの子どもの育成を目指している。
6 サービス紹介
同社の「はなまるサポート」では、若い先生のための授業ヒント集として、毎月の学習指導ポイントを細かく解説しています。また、不明点や疑問点などを無料で相談を受け付けています。
(編集・文責:EDUPEDIA編集部 佐藤 睦)








コメント