1 概要
この実践は(株)教育同人社の許可を得て、「はなまるサポート」の学習指導ポイント一覧より転載しています。
実践の続き(無料)は最下部のURLからご覧ください。
また、以下より実践をPDFでダウンロードできます。
http://www.djn.co.jp/support/special/point/docs/2012/9/2/plan.pdf
2 はじめに
夏休みを過ぎると子どもたちは一段とたくましくなったような気がするのは私だけでしょうか。きっと休み中に心も体も成長するきっかけがあったのだろうと推察します。夏休みは子どもたちにとってかけがえのない成長の機会ですよね。
さて,その成長の場を再び学校に戻しましょう。気持ちも新たに登校してきた子どもたちが,楽しく,わかりやすい授業に臨めるよう,私たちも益々努力しましょう。今回は,多くの先生方が「指導が難しい」「子どもの理解が進まない」と嘆く傾向の強い「単位量当たりの大きさ」を取り上げてみました。参考にしていただければと思います。
3 実践内容
1「単位量当たりの大きさ」という「量」について
長さやかさ,広さ,重さなどの量など,これまでの「量」との違いは何でしょうか。また同じことは何でしょうか。例えば「混み具合」を例にして考えてみましょう。
(1) 直接比較できるか
同じ電車1両目と両目の混み具合は(床面積が同じなので)165人と186人という乗車人数の直接比較で分かります。
(2) 間接比較はあるか
違う型の電車などの場合,混み具合は「定員」と「乗車人数」の割合で求めることができます。その場合の割合は整数、分数、小数などを用いて歩合,百分率,比などで表すことができます。
(3) 任意単位による比較(測定)
6㎡で18人乗ったエレベーターと8㎡で22人乗ったエレベーターの混み具合は,任意単位24㎡当たりに換算して18×4人と22×3人で比較します。これは24単位量あたりの大きさ72人と66人で比較したことになるのです。
また,1㎡当たりの人数を求める方法もあります。つまり,1○○当たりの大きさです。一般にはこの「1○○」を「単位量」,「1○○に当たる大きさ」を「単位量当たりの大きさ」と読んでいます。
このように一方をそろえて比べる仕方には,任意単位の取り方が様々あります。しかし,比較する対象が多く任意単位を公倍数などで求めにくい場合などが多いことから,「1○○」当たりを求めて比較することが多いのです。
(4) 普遍単位による比較(測定)
1○○当たりの大きさを表すものの中で普遍的なものには,人口密度(1?あたりの人口),濃度(異種の2量の重さの割合),速度(1単位時間に対する距離),燃費(1リットル当たりの走行距離),比重(1?あたりの重さ),仕事の速さ(1単位時間当たりの割合)などが挙げられます。すなわち,混み具合などの「量」はこれまで見てきたように2種類の量によって構成されているのです。
2「単位量当たりの大きさ」の比較
以下、T:教師の問い、C:子ども達の答え
(1) 用いる2つの量は何か
例えば,下の表をいきなり与えて「混み具合を調べて見ましょう」という提示はどうでしょうか。これは,当初提示する問題としては感心しません。なぜなら,これでは「花壇の混み具合は「面積」と「本数」で決めなさい」と指示しているようなものだからです。この混み具合は何と何が分かれば比べられるのか,それを指摘することが大切な学力です。
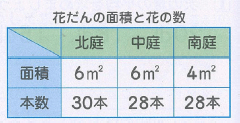
すなわち最初に提示する問題は,むしろ数値が不明な状態でのものが望ましいでしょう。花壇の混み具合なら下図のような提示の方がよいと言えるのです。提示された子どもたちは当然チューリップの本数を数えます。そして北庭,中庭,南庭の広さを知りたいと言うでしょう。そこで「なぜ,花壇の広さが必要なのか」問い,一見しても分かるように北庭と中庭の面積は同じで南庭はそれに比べて面積が小さいことを確認した後,具体的な数値を与えるようにしたいものです。そしてできることなら自分で表に記入する方が望ましいです。
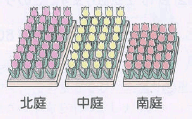
(2) 表から分かること
表から意図的に数値を同じにしているところに着目させます。つまり「この表を見ただけで混み具合が比べられますか」と問うのです。子どもたちは,表と初めに提示された絵を対比させながらこのようなやりとりに進んでいきます。
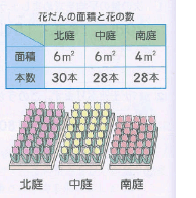
T:この表を見ただけで混み具合が比べられるものがありますか。
C:あります。
C:北庭と中庭です。
C:中庭と南庭も比べられます。
T:それはどうしてですか?北庭と中庭の場合は?
C:面積が同じ6㎡で,チューリップの本数が30本と28本だから,北庭のほうが 混んでいると分かります。
C:同じ面積だとチューリップの本数の多い方が混んでいるからです。
T:面積が同じだと本数で比べられるのですね。
C:そうです。
T:では,中庭と南庭も比べられるのですか。面積が違うようですが。
C:今度はチューリップの本数が同じなので比べられます。
C:同じ28本なので南庭の方が混んでいます。
T:どうしてそれが分かるのですか。
C:同じ本数を広いところに植えるのと狭いところに植えるのでは,狭いところに植えた方が混んでいるからです。
T:本数が同じだと面積の小さい方が混んでいるのですね。
C:そうです。
………
この段階で明確にすべきことは,
- 片方の数値がそろっていれば,もう片方を見て判断できる。
- その値が大きければ?(混んでいる,すいている),その値が小さければ?(混んでいる,すいている)のように,○○ならば△△だと言えるようにする。
ということでしょう。
(3) 表からはわかりにくいこと
(2)から「片方の数値がそろっていれば,もう片方を見て判断できる」ことが分かったわけです。そしてこの考え方をもとにして2つの比較ができました。
- 北庭と中庭は,北庭が混んでいる。
- 中庭と南庭は,南庭が混んでいる。
では北庭と南庭は?ということになりますがこれは表を見ただけでは比べられそうにないということは子どもたちにもわかっています。そこで,
T:北庭と南庭ではどちらが混んでいるか,表を見ただけでは分かりにくいのは何故ですか?

C:面積も本数も数がそろっていないからです。
T:ではどのようにしたらようでしょう。前の2つのように分かりやすく比較にするにはどのような工夫をしたらよいでしょうか。
C:どちらかをそろえればいいです。
(4) 一方をそろえる方法を既習事項から考えること
一方をそろえるには,児童はなるべく数値の小さいもの同士で処理しようとします。そり方が作業が簡単でということを知っているからです。この場合,面積とチューリップの本数という2種類の数値がありますが,30と28の公倍数をとるより6と4の公倍数を取った方が簡単に処理できそうだという見通しを持つでしょう。「方法としては可能でも実際はこのように処理する,それは何故か」を明確にしておいた方がいいでしょう。そして,実際に30と28の公倍数をとつて比較する例も紹介した方がよいでしょう。
T:面積をそろえるならいくつにそろえますか。
C:面積を12㎡にそろえます。
C:北庭は30×2=60本,南庭は28×3=84本なので南庭が混んでいます。
C:24㎡でもいいです。
C:北庭は30×4=120本,南庭は28×6=168本なので南庭が混んでいます。
T:どのように考えて面積をそろえたのですか。
C:6と4の公倍数を考えたのです。
C:30÷6,28÷4をします。
T:これはどんな意味ですか。
C:1㎡に何本かということです。
T:つまり,何をそろえたのですか。
C:面積です。
T:面積をそろえる方法が何種類あるのですか。
C:2種類です。公倍数を使う方法と1㎡当たりで考える方法です。
ここで,気をつけたいのは「単位量当たりの大きさ」とはどちらの方法なのかということです。「単位」とは文字通り「くらべる1かたまりの大きさ」ということです。そう考えると,公倍数の12㎡も24㎡も単位量と言えます。すなわち,
<Aタイプ>
- 12㎡当たりの大きさ…60本と84本
- 24㎡当たりの大きさ…120本と168本
そして,
<Bタイプ>
- 1㎡当たりの大きさ…5本と7本
というふうに,それぞれの単位量に対する値を算出して比べるのです。ちなみにAタイプは「任意単位」,Bタイプはそのほとんどが「普遍単位」として取り扱われています。「どちらが混んでいるのか」の結論は,A,Bどちらの方法でもよいことになります。この段階でのポイントは,あくまでも「単位をそろえる」ということなのですから。
(5) できるだけ一般的にするには
もう一度この表を見ましょう。これは非常に意図的に考えられた数値によって構成されているわけですが,原理を理解した段階でこの比較の方法を問題解決に適用させなければ意味がありません。そこで
- 最初に提示したデータに更に2例ほど加える
- 実際に近いデータを提示する
などして混み具合を調べる機会を作るのです。このことから課題を明確にしていきます。

①2つずつ比べないで一気に全部比べる方法はないのだろうか。

②いちいち公倍数を取るのでは面倒で時間もかかる。公倍数を取らない機械的な方法はないのだろうか。
そこでBタイプの良さが注目されるのです。すなわち「1当たりの大きさ」を求めればよいということに気づかせるのです。
1㎡当たりで比べると,

となり,①②の問題を解決した実感を味わわせることができます。
また,数直線などの数の関係を表すモデルでは,数のように「1」を単位量,「1」の上の数量を「単位量当たりの大きさ」と説明していることもありますが,厳密に言えば「1」は「1単位量」のことです。この「1単位量」の考え方をして共通な比較の方法としているのが,人口密度であり,濃度であり,燃費であり…。これらは言わば「普遍単位」です。
実践の続き
指導で気をつけることなど、続きの内容は下記URLからご覧下さい。
http://www.djn.co.jp/support/special/point/docs/2012/9/2/1.php
4 実践者紹介
初等教育研究所
山﨑 憲 プロフィール
元東京都算数教育研究会会長。
「小学校時代から現在までで,今が最も算数がすき」と,小学校退職後も算数教育に没頭し,現職時代に引き続き年に数回研究授業も試みている。
現在東京学芸大学講師として初等算数科教育法を担当。
またボランティアとして東村山市算数教室を開催し算数好きの子どもの育成を目指している。
5 サービス紹介
同社の「はなまるサポート」では、若い先生のための授業ヒント集として、毎月の学習指導ポイントを細かく解説をしたり、不明点や疑問点などを無料で相談できたりします。
http://www.djn.co.jp/support/
(編集・文責:EDUPEDIA編集部 阿部由和)







コメント