1 はじめに
この記事は、館山市立北条小学校において実践されたものです。北条小学校では昭和37年(1962年)から50年にわたって、「北条プラン」と言われる教育プランを打ち出してきました。北条プランはその間何回にも渡り、試行錯誤が繰り返され改善されています。本実践は「プランⅩ」で平成20年度から行われています。
- 情報共有の要 ~「カリキュラム管理室」の中身を探る~(館山市立北条小学校)
https://edupedia.jp/article/53233f8d059b682d585b6000
2 円と球「どうすればお宝の場所がわかるだろうか」
1.主張
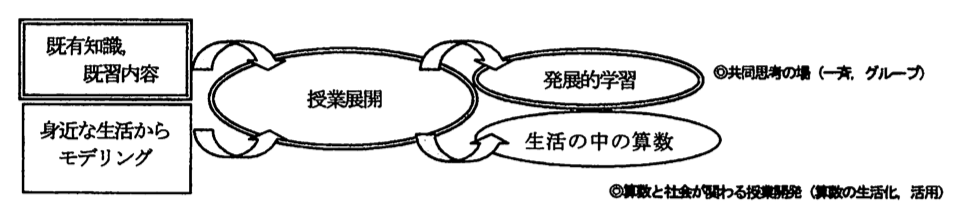
算数って楽しいよ、役に立つのになあ…と身をもって感じ学習していくためにはどのようにしていくのか考えない日は無い。どうしたら、楽しく、算数のカを付けることができるのか。
算数は、学習過程で、一つ一つ謎解き問題のように進めていくことで解答を出せる。そのヒントとして、既有の知識、既習事項がある。それらを活用し、活動を通して自分の考えを持ち,比較・検討の場では算数的コミュニケーションを取り、いろんな考えにふれる。このような学習を積み重ねことで、児童が楽しく、共に進んで学習していくと考える。
そこで大切なのは児童にとって身近な生活場面から興味・関心の持てる学習課題(人、もの、こと)を具体物を用いて設定し「イメージ」を持たせ、主体的に学習が進められるように「算数的活動」 を充実させることだと考える。そこで得た考えを、算数的コミュニケーションを通してさらに深めさせるのである。
2.単元について
(1)教材観
本単元は,学習指導要領 「C (1) 図形についての観察や構成などの活動を通して、図形を構成する要素に着目し、図形について理解できるようにする。」とあり、ウ「円、球について知ること。また、それらの中心、半径、直径について知ること。」とある。
子どもたちはこれまでに、第1学年で「いろいろなかたち」で空き箱や空き缶を使った「積み木遊び」や「形さがし」などの活動を通して、しだいにものの形を認めたり、形の特徴をとらえたりするとともに、筒の形は転がりやすいなどと、ものの形の待機能面も気付いている。また、日常生活の中で「まる」や「まるい形」という表現を平面図形の円や立体図形の球の両方を指して用いている。
本単元では、円と球の定義、そしてそれらをかいたり作ったりすることができるようにすることがねらいである。
また、平面図形の「円」と立体図形の「球」とを分化させ、それぞれの性質の理解を図る。
そのためには興味関心の持てる学習課題を提示し、子どもたち自身が作業的・体験的な算数的活動を通して、円や球の特徴に気付かせ、理解を深めさせながら学習を進めていくようにする。
(2) 子どもの実態
本学級の実態調査の結果は次の通りである。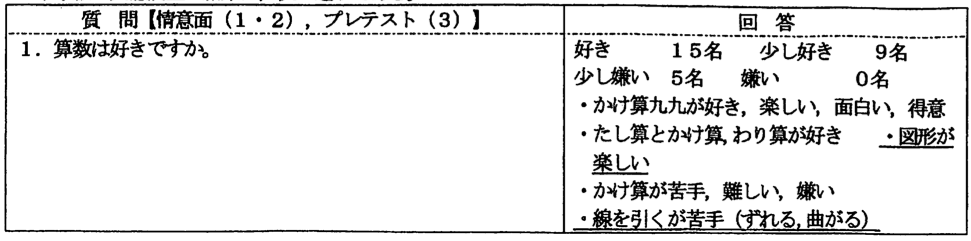
①情意面の調査より
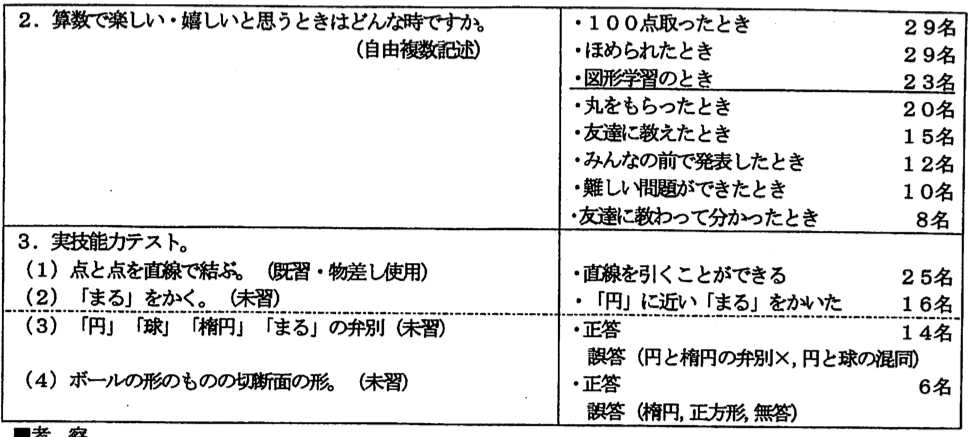
設問1については、24名の子どもたちが「好き・少し好き」と答えている。理由については設問2にあるように、「すごいね・うまいね等ほめられたとき」の喜びつまり認められたという自己存在を感じられたときが喜びとしてあげられている。また、「100点を取ったときの満足感」が多く回答されている。
授業内容にふれている子ども(図形学習が楽しい子ども)は「直線が引けたとき・色旗がきちんと並べられたとき・折り紙でいろんな形を作るのが面白い・三角形や四角形がかける」等技術面での満足感を表していた。その回答からも、図形の授業を楽しみにし、真剣に臨む気持ちを感じる。課題提示の工夫を考え、子どもたちの期待に応えられるようにしたい。
②事前テストより
既習の「かたちづくり」で、点を結んでいろんな形を構成したり、普段から学習課題キ学習問題を物差しを使って線を引いていたりしたことで、直線を引くことはできる。「円」についても真円をかこうと変形しているところを書き直すこともしていた。円と球の弁別もほぼ全員正解であるが、平面図形の円と立体図形の球の区別は十分とは言えない。どちらも「まる」ととらえ、混同している子どもが多い。
(3) 指導観
問題場面のイメージ化【見出す】
本単元では、まず「北条小の宝物」と銘打ち、北条小の平面図を見せ、「3の3の教室から5cmのところにお宝がある」と投げかる。身近な生活場面である自分の学校の平面図を提示するのである。
「どうすれば、お宝の場所がわかるのか」を学習問題とし、「どうしたら解決できるのか」の方策を見出すために、子どもたちの分からないことや疑問を出させる。一人の「?」を全体の「?」としたり、それに対してアイデアを出し合ったりしながら進めていくのである。
解決の見通しが持てた段階で作業的・操作的な算数的活動に取り組んでいくのだが、見通しが持てない子どもについては教師と更に対話を持ち、子どもが何に疑問を持っているのか受け止め、個への対応をしていく。
見通しをもって,作業・操作等の活動【調べる】
「ある点から 5cmの直線を引かせる。」の活動を通して、その直線は無数にあること、円の形になることをおさえる。その形から円の半径、中心、直径の理解をさせる。そして、その定義をもとにコンパスを用いて、作図をするという流れで単元は進んでいく。
常に学習課題やその提示の工夫をし、子どもたちが興味・関心を持ち学習が進められるように作業的・操作的な算数的活動を取り入れ、円の基礎について理解を深めさせたい。
共同思考の場【深める】
本時では、平面図、物差しや定規を用いて作業的・体験的な活動をし、自分の考えを持ち、話し合いを進める。そこには、前時で作業内容を把握し、イメージを持たせ、その活動をもとに、思ったこと・感じたことを出させ、より手早く、簡単にできる方法はないか話し合わせるところに意図がある。作業イメージとは、自分で操作したこと(物差しを回転させたり、作業プリントを回転させたり、5cmの長さを紙に写し取ったり等)である。
そこから得た線を引く順序性、よりよい方法等の考えを共有し、イメージを持って作業することができると考える。
この時間を発表会にするのではなく、困っていることを出させたり、自分のできたところまで発言させたりして、そのあとをみんなで考えていくという形を取る。また「どうしたらできるのか」「何をすればよいのか」も共に考えられる共同思考の場を大切にし、学習させていきたい。
ふり返り【まとめあげる】
毎時間最後にふり返りの時間を取る。算数日記と銘打ち、ノートに書いたり、発表したりする。ノートには 「学習課題→学習慣髄→自分の考え→友達の考え→まとめ」があり、それらを見たり、授業をふり返ったりして、「わかったこと・気づいたこと・まだ疑問に残っていること・次にやりたいこと」等を書く。それらを共有するために教師が見て回り、発表を促す。どのように表現すればよいのかわからない子どもへの一助ともなる。
ここでは「自分と友達は同じように考えているんだ」とか「そういう考えもあるんだ」等、気持ちのつながりを感じ取ることもできる時間としたい。
TT指導について
子ども一人一人にあった指導ができるように、3年算数科では、週2時間TT指導を実施している。課題提示では、子どもたちがイメージを持ちやすいように2人で実演を入れることもある。学習課題がのみ込めない子ども、作業が不得手な子どもには、分かれて個別支援にあたることができる。また、自力解決の時間には子どもたちの考えを把握したり、相談を受けたりしながら、よい考え(話し合いが成立する内容等)は積極的に吸い上げ、意図的指名に繋げることもできる。何よりも子どもたちのことを考え、一人一人の考えを大切にすることができることが、TT指導の良さと考える。
3.単元のねらい
○円や球の概念について基本的な事項を理解し、コンパスを使って円をかいたり長さを写し取ったりすることができる。
- 身のまわりにあるまるいものに関心をもち、共通の性質を理解しようとする。(関心・意欲・態度)
- 「まるい形」という感覚を、円、球という数学的概念に深めることができる。(数学的な考え方)
- コンパスを使って円をかいたり、長さを比較したりできる。(表現・処理)
- 円や球、およびそれらの中心、半径、直径の意味を理解できる。(知識・理解)
4.単元全体のプラン(12時間扱い)
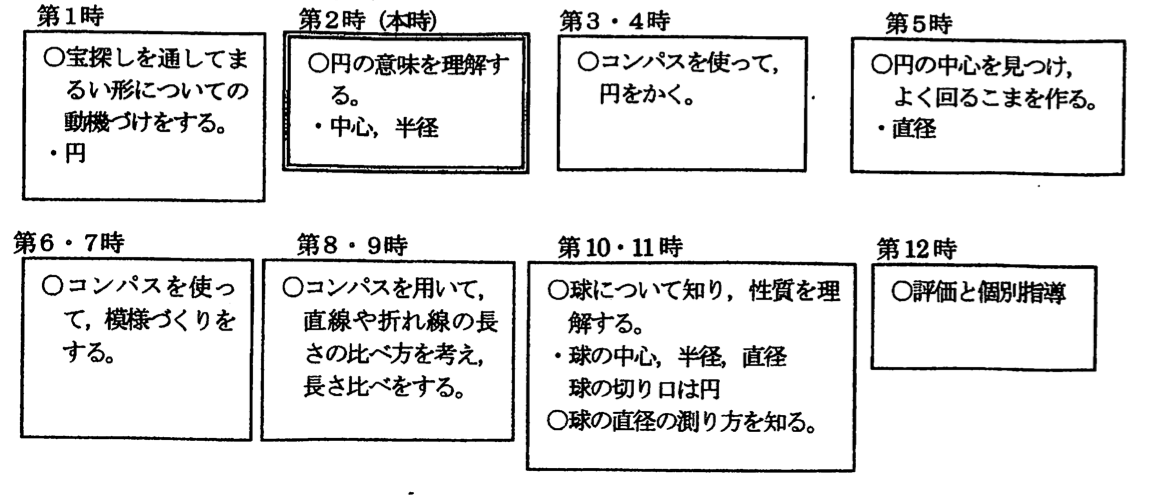
- くわしくはこちらの記事へ
https://edupedia.jp/article/56541efe903a84000012357d
本時の指導(2/12時間目)
(1)本時のねらい
- 自分の考えをもって直線を引く操作活動を通して、円の意味を理解する。
- 「中心・半径」の用語を知る。
(2)展開

3 「館山市立北条小学校」というキーワードの関連記事
- 北条小の他の実践はこちらからどうぞ
⇒https://edupedia.jp/articles/keyword/54085b89ddab6dc46ef32013







コメント