1 はじめに
本記事は、2019年2月25日(月)に開催されたイベント「逆向き設計で考える『学びの深化』〜マトリックス思考で学びを深くするには?」(主催:Teacher’s Lab)の内容を編集・記事化したものです。本イベントでは、マトリックス思考で学びを深める方法を講師のShingo Noguchi先生にお話しいただいたあと、ワークショップ等が行われました。本記事では、先生がお話された部分についてご紹介します。
2 マトリックス思考の例
やる気とスキルのマトリックス
私は何事もマトリックスで考えるのが好きです。
たとえば自分のクラスの子どもたちについて、このマトリックスで考えています。
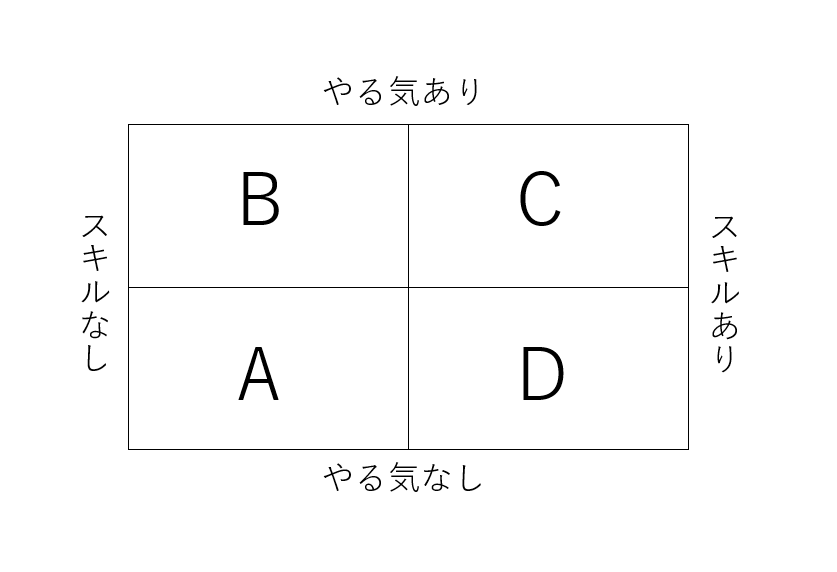
子どもとの相性もありますが、
・やる気がなくて勉強もできない子であれば、まずはやる気にさせる必要があるので、勉強が楽しくなるような動機づけをしたい(A→B)
・やる気はあるけど勉強はできないという子であれば、勉強をできるようにしてあげたい(B→C)
・勉強はできるけどやる気がないという子であれば、リーダーを任せるなどして自信をつけてあげたい(D→C)
という風に考えています。
このように「良い子・悪い子」「できる子・できない子」という見方だけでは見えなかったものが、マトリックスを使うことで分析的に見られるようになります。そうすると自分のすべきことが決まりやすくなるのです。
子どもの主体性と先生によるガイドのマトリックス
他にも私がよく使うのが、このマトリックスです。
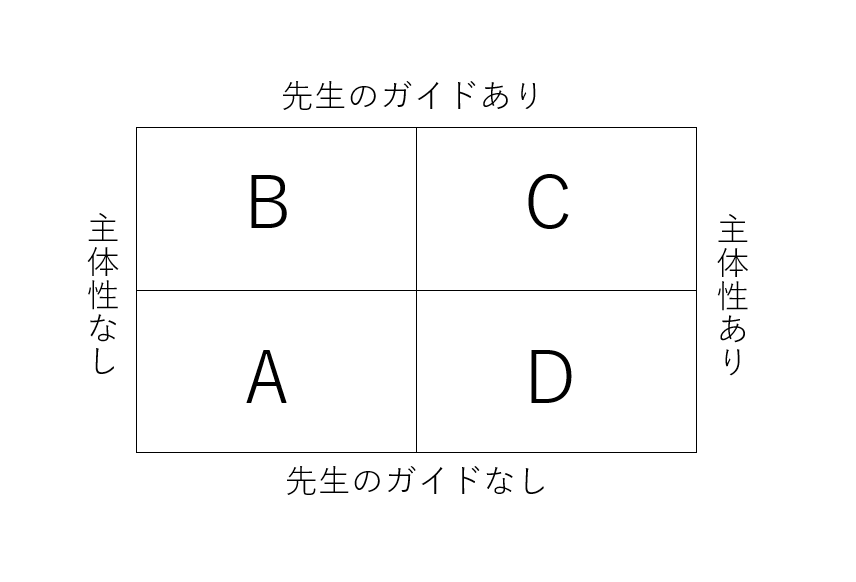
先生のガイドというのは、先生のねらいや、導きたい方向のことを表しています。
たとえば、主体性を意識しすぎて子どもたちのやりたいことばかり自由にやらせてしまい、学習指導要領の内容が網羅されていないような授業は図のDにあてはまります。
Bにあてはまるのはいわゆる詰め込み学習で、Aは子どもたちの主体性も先生のガイドもない無法地帯です。
そして、Cの状態が私たちの理想です。そこまでどのように持っていくか、ということが今日のテーマになります。
3 学びを深めるマトリックス
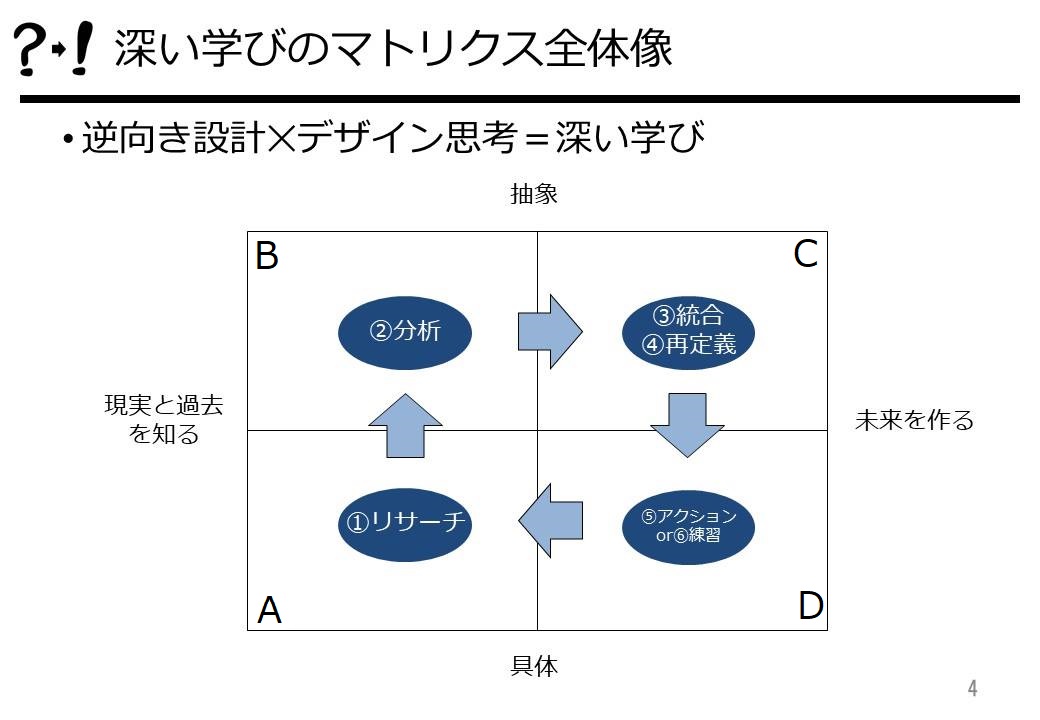
この図が、今回お話する内容のすべてです。
ここで表されているのは「現在や過去の具体的なことからスタートして、それを一度抽象化し、そこからさらに具体的に次のアクションを考える(A→B→C→D)」という、学びを深めるための一連の流れです。
深まらない学びの例
たとえば算数の授業で、「13.6mのテープがあります。このテープから3mのテープは何本取れて、何mあまりますか。」という問題を学ぶとします。ここで13.6÷3の計算(A)をしたあとに練習問題を解く(D)だけでは学びが深まりません。
また探究の授業で「沖縄の調べ学習をしましょう(A)」「次に京都の事を調べましょう(D)」というだけではやはり学びは深まりません。
つまり、図のA→Dというように、具体的に何かをして次にやることを考えるだけでは学びがまったく深まらないのです。
深まる算数の授業の例
私はいま小3の算数の授業で「わり進む計算」と一緒に、4年生の内容である「あまりのある計算」も教えています。なぜかというと、はじめに「わり進む計算をやるよ」と言って子どもに解かせて、次に「あまりのある計算をやるよ」と言って解かせると、結局子どもたちは「どういうときにわり進むのか」「どういうときにあまりを出すのか」が分からなくなってしまうからです。ですから最初にあえて2つの分野を一緒に教えることで、子どもたちを混乱させ、「じゃあこれはどっちのパターンかな?」と、分類する力を身につけさせることができます。このようにして、学びが図のA→B→Cという風に進むのです。さらにそれを子どもたちの頭の中で統合させて、もう一度Dの具体的な部分に戻ってくることで、子どもたちは「この問題とこの問題ってここが違うんだね」とある程度認識できるようになるのではないかと思います。
深まる探究の授業の例
実はこの図は国際バカロレア(IB)の「逆向き設計」という考え方にも関わっています。具体的なことを教える前に、先にCの部分を決めておきましょう、という考え方です。

たとえばこれは小3の探究の授業について書いたもので、上に大きく「技術は知識の組み合わせで発展する」と書いてあります。これがCの部分です。
でも小学校3年生にいきなり「技術というのは知識の組み合わせで発展するんだよ」と言ったところで、何も分かりませんよね。
だから最初は、抽象的なことを教える前に「偉人を調べてみよう」とか「電池の直列・並列つなぎをやってみよう」という風に具体的なものを調べさせます。
以下の画像が実際に使用したワークシートです。

このワークシートには様々な仕掛けが作ってあります。
たとえばグラハム・ベルは、もともと聴覚障害者の人とコミュニケーションを取る方法を研究している教師で、試行錯誤しているうちにたまたま失敗から電話を発明しました。実はそこに電気が関わっていたのだということを知った子どもたちは、「あ、電話を発明する時も電気って関係あったんだ」と気づくわけです。そうやって具体的なことをいくつか調べていくなかで、「あ、今までの発明って知識の組み合わせだったんだなあ」となんとなく分かっていきます。
さらに、小学3年生の国語では大事なところを押さえたり、要約したりすることに重きを置いているので、偉人をただ調べて終わりにするのではなく「グラハム・ベルはひとことで言うとどんな人なのか」といったことをまとめさせています。
また、国際バカロレアの言葉で「Learner Profile」というものがあります。これは「Thinker」「Risk Taker」など、国際的に活躍するための理想の人物像に関する項目がいくつかまとめられたものです。偉人調べをしながらこれらの項目と照らし合わせて、「この人はどの項目が当てはまるのかな」と考えさせるようにすることで、偉人調べが「目的」ではなく「手段」に変わっていきます。
このような流れで、子どもたちはCの部分を学んでいきます。いきなりCの部分を教えるのではなく、まずは具体的なところに落とす必要があります。このように、AとCの両方を考えるということがとても大事なのです。
ちなみに、この抽象化するときのパターンは田村学先生の「深い学び」という本に詳しく書いてあります。(田村学先生についての記事はこちら)
Cの部分を学んだ後に、次はDの部分として、「じゃあ自分たちがRisk Takerになるためには、教室の中で何ができるかな」と考えていきます。
4 マトリックス思考の活用
仕事でもこのマトリックス思考を活用することができます。
たとえば教材研究をするとき、次回の授業の範囲の教科書や指導書だけを読みこむのはA→Dの考え方です。そうではなく、学習指導要領を読んだり、他の学年とのつながりを把握したりすることで、Bの部分に行くことができます。
他にも、サラリーマン時代には「コピーを取って」と具体的に指示された時に、その目的を考えて「お客さんに出す資料はカラーコピーをするけれど、社内向けの資料は白黒でツーアップにしよう」という風に具体的な行動を変えていました。これも、ただ言われたことをやるのではなく、一度BやCの部分を考えるということです。
このような考え方を、子どもたちにも身に付けてほしいと思っています。
5 講師プロフィール
Shingo Noguchi 先生(開智望小学校教務主任)
曾祖父、祖父、父すべて教員の4代目。茨城県守谷にある私立小学校の教員。大学ではデンマークやフィンランドの教育システムを研究。キャリア教育や生涯学習に興味を持つ。
NPOカタリバに参加し、30校以上の高校へ行き、3000人以上の高校生と接する。
大学卒業後コンサルティング会社に入社。人材開発領域のプロジェクトに多数参加。新入社員育成やOJTの仕組み構築などを経験。その後独立し個人事業主としてネットショップ経営、個人コンサルティングなどを経験。通信教育で小学校教諭一種免許状を取得。
開智学園総合部に勤務後、開智望小学校開校準備室にて業務を行う。2018年4月現在は開校4年目を迎えた開智望小学校で教務主任と3年生主任を担当。学校外では、菊池省三先生や沼田晶弘先生、コーチングセミナーや教員サークルに頻繁に参加。公立の教員の知り合いが多く、積極的に交流を図っている。
趣味は読書で1日1冊は本を読む。累計読破数は4,000冊以上。
開智望小学校 HP 開智望小学校 Blog
(2019年2月25日時点)
6 Teacher's Schoolについて
Teacher’s Schoolは、下の3つの価値を大切にしながら、学校の先生と共に様々な社会資源を活用し「学びたい先生が主体的に学べる環境」「挑戦したい先生が自分のやりたい事に挑戦できる環境」の創造を目指しています。

Teacher's School 3つの価値
つくることで学ぶ「生成的な学び」
ふりかえることで学ぶ「内省的な学び」
つづけることで学ぶ「継続的な学び」
失敗を気にせず自由に試行錯誤して、自分の想いを「学び」のプログラムにすることができるのが特長です。
詳しくはこちら↓
HP:teacherslab 、Facebook
HP:Teacher’s Schoole
Mail:info@teachers-lab.org
7 編集後記
この後のワークショップでは、今回のマトリックス思考を活用して参加者自身の身近な課題を分析しました。このときに出てきた「このマトリックス思考で授業づくりをしていると余裕が生まれる」というお話がとても印象的でした。様々な場面で活用できるこの考え方を、私も取り入れてみようと思います。
(取材・編集:EDUPEDIA編集部 平原由羽)








コメント