表からきまりを帰納的に見いだし,そのことを活用する事例
この実践は文部科学省から許可を得て、文部科学省ホームページ上の「先生応援ページ」より転載させて頂いております。ここから指導案もダウンロードできます。添付ファイル
単元の目標
体積の意味や測定及びその単位について理解し,立方体や直方体の体積を求めることができる。
本時の目標
伴って変わる二つの数量の関係を理解し,表からきまりを見いだし活用して問題を解くことができる。
本時の評価規準
【数学的な考え方】 数量の表を観察して,一方が,2倍,3倍,4倍,…になれば,他方も2倍,3倍,4倍,…になるなど,二つの数量の対応や変わり方の特徴を見いだしている。
主な学習活動
◎指導計画における本時の位置づけ(全11時間)
- 第一次 体積の表し方(6時間 本時6/6)
- 第二次 体積の単位(3時間)
- 第三次 学習内容の定着とまとめ(2時間)

指導事例と学習指導要領との関連
小学校学習指導要領・算数の第5学年では,内容「D数量関係」「(1)表を用いて,伴って変わ る二つの数量の関係を考察できるようにする。ア 簡単な場合について,比例の関係があることを 知ること」を示している。
表に表したことを読み取り,きまりを見いだし説明することも算数における言語活動である。
本事例における言語活動は,表に表したことを基にきまりを見いだし説明する活動である。児童 は,これまでに伴って変わる数量について,表に表し,変化の様子をとらえることを学習してきて いる。本時は,このことを活用する。一方が2倍,3倍,4倍,…になるとき,もう一方も2倍, 3倍,4倍,…になる関係は比例関係であるが,このような関係は今までも場面としては出てきて いる。本時では,表から見いだしたこの考えを活用する言語活動を行った。算数の学習では,言葉 だけではなく,数,式,表,グラフを用いて表し,そのことから考えを深めることが言語活動とし て大切な活動である。
言語活動の充実の工夫
表から帰納的にきまりを見いだし,きまりを基に問題を解決する。(*1)
本事例においては,表から帰納的にきまりを見いだし説明する言語活動を取り入れることで,きまりを活用する力を高めようとした。
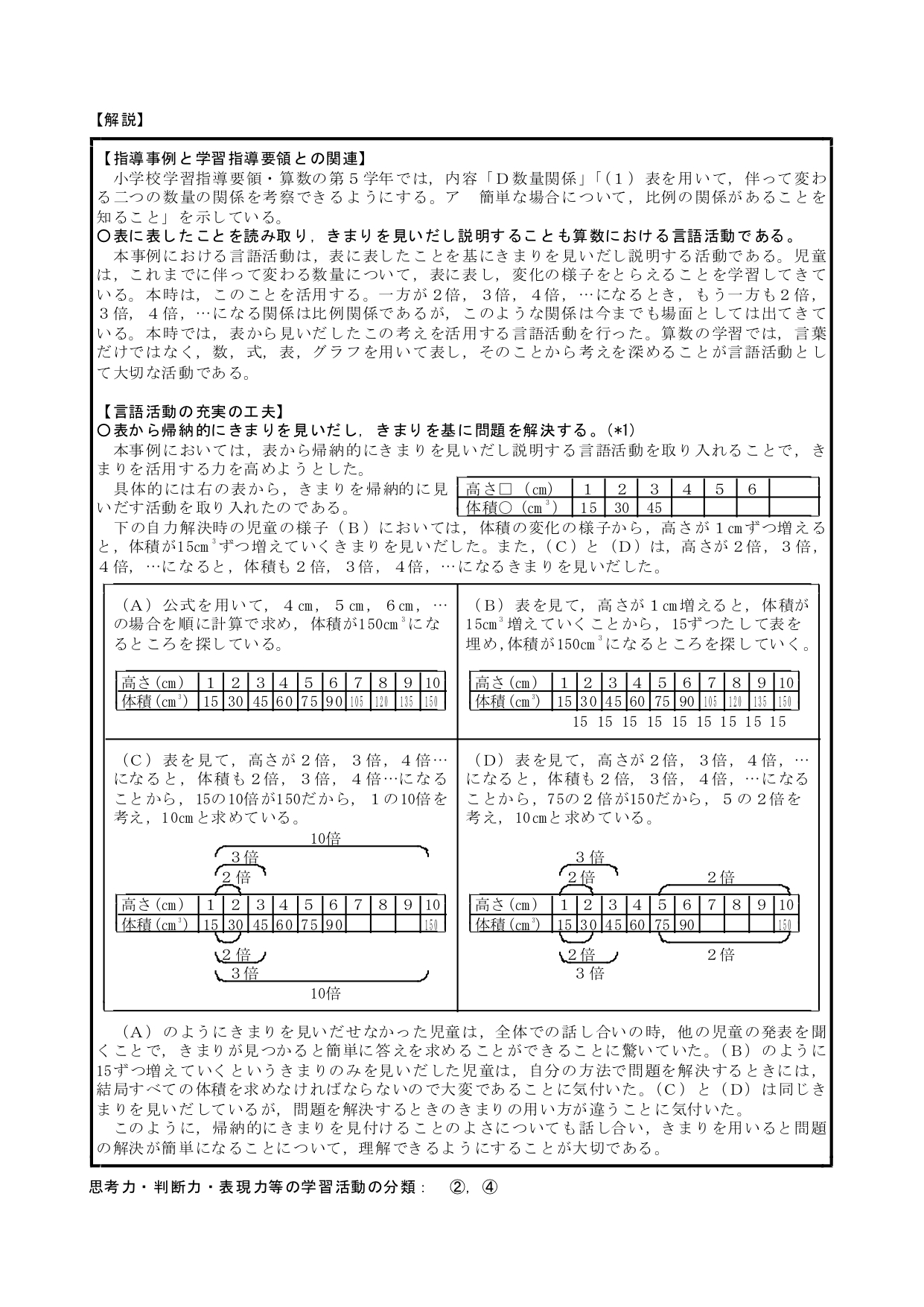
具体的には右の表から,きまりを帰納的に見いだす活動を取り入れたのである。下の自力解決時の児童の様子(B)においては,体積の変化の様子から,高さが1cmずつ増える と,体積が15cm3ずつ増えていくきまりを見いだした。また,(C)と(D)は,高さが2倍,3倍, 4倍,…になると,体積も2倍,3倍,4倍,…になるきまりを見いだした。

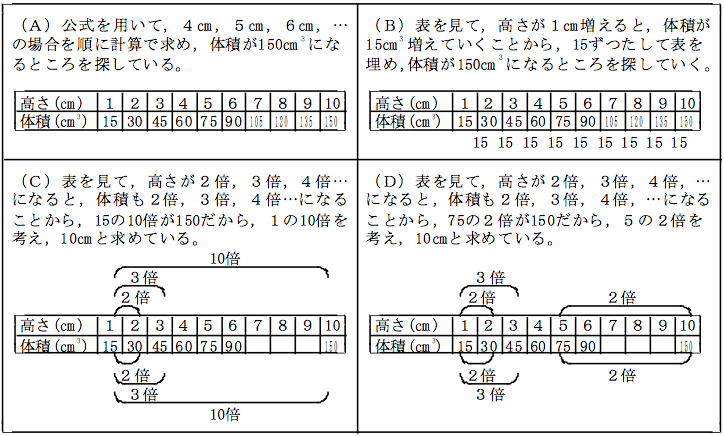
(A)のようにきまりを見いだせなかった児童は,全体での話し合いの時,他の児童の発表を聞 くことで,きまりが見つかると簡単に答えを求めることができることに驚いていた。(B)のように 15ずつ増えていくというきまりのみを見いだした児童は,自分の方法で問題を解決するときには, 結局すべての体積を求めなければならないので大変であることに気付いた。(C)と(D)は同じき まりを見いだしているが,問題を解決するときのきまりの用い方が違うことに気付いた。
このように,帰納的にきまりを見付けることのよさについても話し合い,きまりを用いると問題 の解決が簡単になることについて,理解できるようにすることが大切である。

引用元
文部科学省ホームページ「先生応援ページ」(授業資料・学習評価等)
http://www.mext.go.jp/a_menu/shotou/new-cs/senseiouen/index.htm







コメント