くどいぐらいに 6×5=6×4+6 の、パターン
かけ算の学習時には、1~9段の各段でくどいほど特徴を考えさせられます。基本的には
◆ かける数が1つ増えると、答えはかけられる数だけ増える・・・ 3×5=3×4+3
というパターンの繰り返し。九九はたし算の暗記であるのだから、
3×5=3+3+3+3+3=(3+3+3+3)+3=3×4+3
でしょう。ほかにも、時々、面白い特徴が見つかることがあります。
たとえば、
◆ 9の段で答えが 09・18・27・36・45・54・63・72・81・90 と、商を横並びに見てみると、左右が対称になる。
まあ、そんな授業を、1つの段に1時間かけながら、グダグダとやっています。
九九の表の特徴
そして、最後には九九の表を出してきて、またもや特徴を探します。教科書的には
◆ かける数が1つ増えると、答えはかけられる数だけ増える・・・ 3×5=3×4+3
◆ かけられる数とかける数を入れ替えて計算しても、答えは同じになる・・・ 6×9=9×6
の2つを押さえておけばいいのだけれど、これでは1時間がスカスカな気がします。
そこで、「他にもいろいろ特徴があるから、探してみましょう」と、子供たちにけしかけてみます。宿題で考えさせてもいいと思います。例として、同じ数をかけたものの商が表の対角線にある事を示します。下図のようなプリントを配ってあげると、何パターンも考えてくる子供がいます。
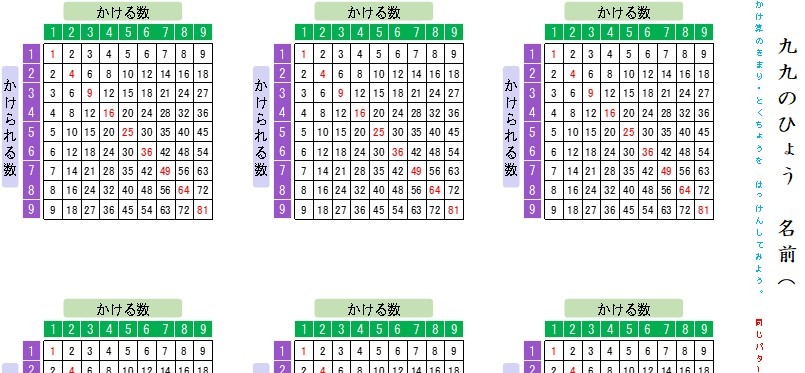
まあまあ面白い考えが返ってきますし、中にはこちらが驚くような考えを発表する子供もいます。
◆ 「2つの同じ商 7×2と2×7」「3つの同じ商 ex.8×2と2×8と4×4」「4つの同じ商ex.6×4と4×6と8×3と3×8」「同じ商がない ex.3×3」などの、パターンがある。
◆ 3の段と6の段の商の和は、9の段の商になる。3×5+6×5=9×5(このパターンは多数)
◆ 4の段の商(任意)の上下左右の商を足すと、商の4倍になる。(全部、そうなんだけどね)

例:4+12+6+10=32=8×4
◆ 真ん中の2乗を線に見立てて交換法則が成り立つ商は、互いに線対象の位置にある。
・・・線対象については、パワーポイントで、下図のように変化するスライドショーを作ってみたので、添付ファイルをご覧ください。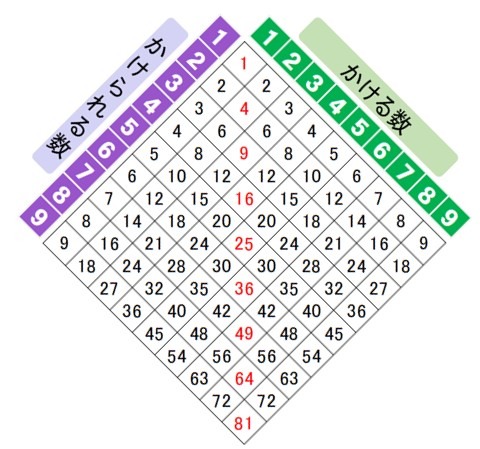
九九の表で見ると線対象に気が付きにくい子供でも、表を45度回してあげることで、鏡のようになっていることが理解しやすいと思います。
宿題にしたので、おそらくお家の方も子供と一緒になって一生懸命考えてくれたようで、ちょっと小学校2年生の授業で扱うには難しすぎる考えもたくさんありましたが、けっこう面白い時間になりました。下記リンク先もご参照ください。
こうした考えさせる授業も必要ですが、何と言ってもかけ算の学習には九九の暗記がメインテーマになってきますね。下記リンク先等を、是非ご参加ください。










コメント