1 難関「小数倍」「割合」
下記リンク先も是非ご参照ください。しっかりとスモールステップを作って「詰める」ことによって、けっこうな難問も含んでいるテストでクラス平均85点を記録しました。
子供たちが躓く所は、「小数倍」と「割合」でしょう。小数で割るという感覚が身につきにくい、あるいは「もとになる数」「比べる数」の区別がつかず、何÷何であるかがつかめないといったところが子供たちが苦手とするところだと思います。子供たちの混乱
に引きずられて、教える側の教員も混乱してしまうことがあります。
・
一般的には「もとになる量」「くらべる量」「割合」という言葉を使って説明をしているのですが、これがまた、子供にはピンときません。「もとになる量」は、「基準の量」とでも言いかえた方がはっきりしていいような気がしますが・・・。「もとになる量」「くらべる量」「割合」をはっきりつかめるなら、「くもわ」を下図のように書かせると、求めたい量を隠したときに、く=も×わ、も=く/わ、わ=く/もとなって、簡単にわかります。
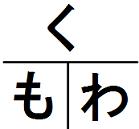
・
しかし、「くらべる量」を求める場合に、1以下の数で割ることが出てくるのが難しいのです。どちらが基準なのかを見極めるのも難しい。私も教えていて時々混乱してしまうことがあります。「もとになる量」「くらべる量」がどちらなのかを理解しにくい子供は多いです。さて、この難関をどう乗り切るかです。
2 計算は電卓を使わせる
算数の授業での電卓の利用については色々と議論はありますが、文章題が苦手な子供は計算も苦手である率は高いです。割合の理解と計算という2つの要素を持ち込めば正答率が低くなり、やる気も失せてきます。混乱をするのは当然です。とにかく、割合の理解を優先させ、計算は十分に理解ができた後にできるようにさせればいいのではないかと思います。
3 小数倍から入る
小数倍・百分率・割分厘・分数を教えなくてはなりませんが、百分率・割分厘・分数は、小数倍を徹底してからやればよいと思います。百分率・割分厘ともに小数と同じ意味であり、あせって3者を次々と持ち出すと、子供は混乱します。「75%は0.75倍」、「3割2分5厘は0.325倍」の事だと教えておけば、後は楽々です。ちなみに新学習指導要領の下、割分厘は小さく扱われるようになっています。
4 文章の中から、○は○の○倍を見つける訓練を繰り返す。
割合は、「もとになる量」「くらべる量」「割合」が問題の中に書かれてあって○は○の○倍という形で3つの量の関係を簡単な言葉で把握できるかどうかが攻略の大きなポイントです。
・
幸子さんの市の小学生の数は、8190人で、これは、市の人口の0.08倍にあたるそうです。市の人口は、何人でしょう。
・
この問題であれば、次のように内容を把握させていきます。
(1)市の人口の0.08倍は、小学生の数
↓
(2)市×0.08=小
↓
(3)□×0.08=8190
↓
(4)□=8190÷0.08
↓
(5)□=102375
・
(1)は指示語「これ」を使っていて、「小学生の数」に直すのが難しい子供もいます。他にも、「○は○の○倍」の形でそのまま文章中に書かれていないパターンもあり、そんな場合には子供は混乱しますが、上手に読み替えるように練習させましょう。
・
(1)が把握できた時点で、
・
「は(が)」は「=」
・
「の」は「×」
と、教えておけばすぐに(2)の立式へと進むことができます。
問題を解くときには、を必ず書かせるようにします。□(求める数)は「もとになる量」「くらべる量」「割合」のどれかになるわけですから、問題の数字を当てはめると、(5)の時点で、□=30×0.4 12=□×0.4 12=30×□ と、3つのパターンにしかなりません。一つ目はかけ算そのままなので楽勝ですね。2つ目、3つ目の□を求めるには、「かけている数で割る」でいけます。
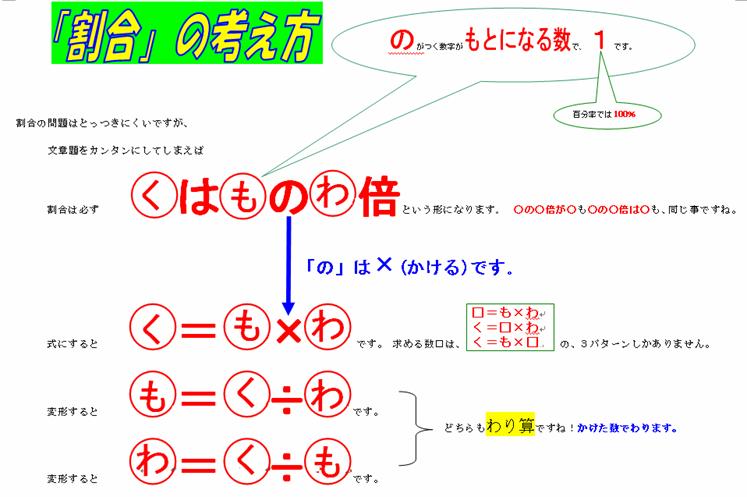
5 指導を徹底する
塾や家庭等で先行して学習していて、他の形での解法に慣れている子供はこのやり方を嫌がることがあります。しかしその子供達に「何でもいいよ」と言ってしまえば指導はあいまいになってしまい、どの子が自分のやり方で理解できていてどの子が自分のやり方でなかなかはかどらなくなってしまいます。とりあえず、指導をやりきるまでは、全員に徹底しましょう。先行経験があるような子供は、もともと柔軟性があり、最初は文句を言っていてもすぐに慣れます。
6 割合が「1」より大きいかどうか
割合が「1(百分率なら100)」より大きいかどうかによって、結果を予想・判断するセンスを身につける。又は、「もとになる量」と「くらべる量」がどちらが大きいかによって割合が「1(百分率なら100)」より大きいのかによって、結果を予想・判断するセンスを身につける。
7 色々な方法で感覚的につかめるようにさせる。
「1.5」で「指導を徹底すると」書きましたが、○は○の○倍という解法の型にはめ込むのがベストなのかどうかと聞かれるとちょっと自信がありません。ある意味機械的で簡単すぎて、子供の考える機会を奪っているような気もします。
絵や線分図、その他の方法を用いて、やる事を否定しているわけではありませんし、それぞれに対応できる柔軟性は必要だと思います。○は○の○倍で教えるだけではなく、色々な解法、考え方を身につけさせる必要があると思います。




コメント