三角柱・四角柱・円柱　～柱体の表面積　6年算数　（シリウス）

2025 8/26

1　はじめに

こちらの記事は、静岡県で30年間以上続く教員サークル、シリウスのホームページに掲載されている教育実践法の一つをご紹介しています。

シリウスのホームページはこちら→　静岡教育サークル／シリウス

是非、下記リンクもご参照ください↓↓↓。

ジュースがたくさん入る入れ物は？　～立体の体積（シリウス） | EDUPEDIA

2　実践内容

柱体の表面積の学習をおこなった。三角柱・四角柱・円柱とも

立体の表面積＝底面の表面積＋側面の表面積

であるから、グループ別に考えた。（教師は３人で３つのグループにわかれる。）求め方がわかったところで、それぞれの表面積の求め方を紹介しあった。まず、３つの立体を提示して、

発問１

ここに３つの箱があります。ペンキを塗っていくのだけれど、ペンキの量をなるべく少なくするためには、どの立体が一番少なくなるでしょう。見た目でどれが少ないか決めましょう。

用意した立体は、次のものである。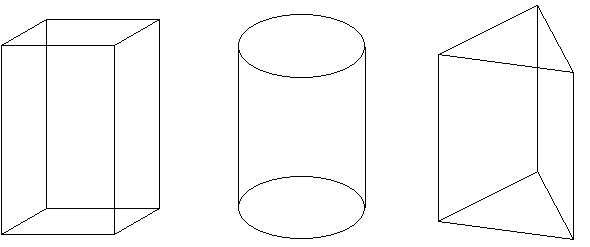

立体を見ただけでどれが一番ペンキが必要かを考えさせた。３つの立体を比べるときに、次のことを確認した。

・ペンキを塗る量は、表面積を調べればいいこと
・三つの立体の表面積をそれぞれ出したあと、一斉に比べる

発問２

１つ立体を選んで、どのくらいペンキを使うかグループごとに検討しよう。

子どもたちの予想は、次のようにわかれた。円柱と考えた子が一番多かった。

< 三角柱 > 15人　< 円柱 > 36人　< 四角柱 > 20人

三角柱グループは、表面積の求め方について、次のような話し合いをした。

< 三角柱 >　15人

Ａ：すべての面の面積をそれぞれ出す。
Ｂ：展開図にして、三角形と長方形の面積をそれぞれ出す。

「もっと簡単に計算したらいいのではないかなぁ」という声があがったので、もっと簡単な方法がないか考えた。

・底面積は底面積で求める。側面積はバラバラに求めないで、展開図で考えるといっぺんに求めることができます。
・三角形のまわりの長さは側面積の横の長さと同じになるから、三角形のまわりの長さ×三角柱の高さをすれば、側面積が出ると思います。

それぞれのグループの表面積が出たところで、求め方を紹介しあった。

指示１　自分たちのグループが、どのように表面積を求めたか教えてください。

< 三角柱 >　15人

・一面ずつ計算するのは面倒なので、展開図で考えました。展開図にすると、三角形と長方形になります。それぞれの面積は

三角形：　９× 12÷２が２つで 108 c㎡
長方形：　10×（９＋12＋15）　306 c㎡
合計で： 108＋360 ＝ 468 c㎡

< 円柱 >　36人

・円柱も形は違うけれど、出し方の基本は同じです。教科書p21に式があるんですけど底面積×２＋側面積で底面積は２つなので

円　：　５×５×3.14が２つで　157 c㎡
長方形：　10×（10×3.14）　314 c㎡
合計で： 157＋314＝471 c㎡

< 四角柱 >　20人

・四角柱も展開図にしました。底面積が２つあるので、側面の長さは８cmが４面なので８×４

正方形：　８×８が２つで　 128 c㎡
長方形：　11×（８×４）　 352 c㎡
合計で： 128＋352 ＝ 480 c㎡

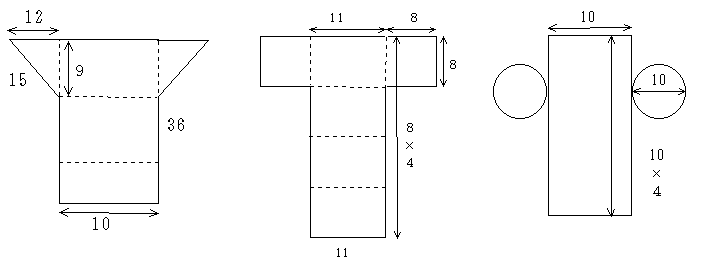
３つの立体の表面積を比べると、三角柱が一番小さいことがわかった。

結果は、三角柱：468 c㎡，円柱：471 c㎡，四角柱：480 c㎡であった。それぞれの面積を求めたあとで、共通点について尋ねてみた。

発問３

立体の表面積を求めるときに、似ているところはありましたか。

・展開図に直すこと
・底面が２つあること
・円と長方形、三角形と長方形、四角形と長方形のように、底面の形と長方形というように簡単な形になっている。

指示２　今から練習問題をしてみよう。自分が求めた以外の立体の計算をしよう。

底面の面積は求められるのだが、側面の面積が難しかった。立体の高さ×横の長さのうち、横の長さがよくわからないのである。

三角柱：三角形の各辺の合計
四角柱：四角形の各辺の合計
円柱：直径×3.14

この関係を十分把握させることが必要だと感じた。

3　プロフィール

静岡県教育サークル　シリウス

1984年創立。
「理論より実践を語る」「子どもの事実で語る」「小さな事実から大きな結論を導かない」これがサークルの主な柱です。
最近では、技術だけではない理論の大切さも感じています。それは「子どもをよくみる」という誰もがしている当たり前のことでした。思想、信条関係なし。「子どもにとってより価値ある教師になりたい」という願いだけを共有しています。