ありの近道はどの道か　～立体　小学校6年算数（シリウス）

2025 9/06

1　はじめに

こちらの記事は、静岡県で30年間以上続く教員サークル、シリウスのホームページに掲載されている教育実践法の一つをご紹介しています。

2　実践内容

立体の展開図の授業をおこなった。ありが歩く近道をさがす中で立体の展開図に気づかせる授業である。子供たちの知的好奇心をくすぐりたい。

【発問１】ありが図のように下の端にいます。上の端に砂糖があるとき、どの道を通っていくのが一番近道になるでしょうか

実際に立方体を触りながら考えることにした。近道だと思われるところには鉛筆で線を引いてみた。子どもたちが試した方法は次のものだった。実際に立方体を触りながら考えることにした。近道だと思われるところには鉛筆で線を引いてみた。子どもたちが試した方法は次のものだった。

・線引きで長さを測る
・ひもで長さをくらべる

考えられたコースは次の４つであった。

Ａ：底面→側面→底面と辺の上を移動する
Ｂ：側面は辺上、底面は対角線上を移動する
Ｃ：側面は対角線上、底面は辺上を移動する
Ｄ：側面、底面とも対角線上を移動する

【発問2】線引きやひもでは、目印の位置がずれたりしませんか。また、立体の角が削れたりしていて、正確な長さを測ることができませんね。正確な長さを測るためにはどうしたらいいでしょう。

実直方体・立方体の展開図については、５年生のときに学習している。このことを思い出して展開図について気がついた子がいた。

展開図を考えていたんだけれど、スタートからゴールまで一番近いのは直線で結ぶのが近い。だからＤが一番近いと思う。
ひもの長さで測ってみたんだけど、Ａのように辺を通っていくのは31cm、Ｂのように斜めと一辺は25cm、Ｃのように斜めにいくと20cmだった。
どの道が一番短いかは、展開図を書いて書いてスタートゴールの点を結ぶのが一番近いと思う。

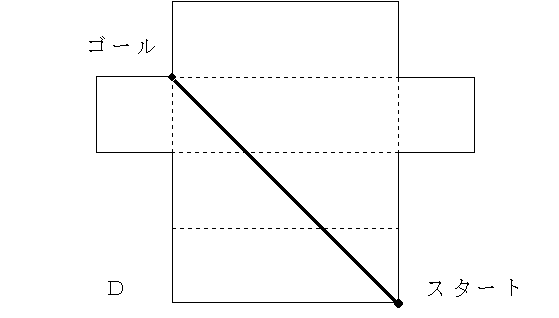
ここで質問が出た。斜めに引く線が辺上で交わる点についてである。斜めの線は位置がずれてしまうかどうかについて検討することにした。

【発問３】一番の近道は、ななめの線を引くことだと言っているけれど、その辺上で交わる点Ｇダッシュは、中途半端な位置だからずれてしまうんじゃないですか

< 位置がずれてしまうことはない >

Ｏ君と同じで展開図を書いて、端から端までの点をまっすぐに結べばいいと思う。
展開図を書いて、点から点へ結ぶのだから、まっすぐに引くことができます。
教科書にも立方体の展開図がありました。点の位置を決めてまっすぐに引けば、一番近い距離がわかる。だからずれることはない。

また、この斜めの道にも２種類あることがわかった。

斜めの線がいいと思います。展開図を書いてみたんだけれど、太線は９cm、点線は 8.4cm で６mm 違いました。
Ｄの斜め線にも２種類あることがわかりました。展開図を書いてみたんだけれど、太線は 6.5cm、点線は７cm でした。組み立てるとどちらも同じゴールに行くので、太線の方が近いことがわかりました。

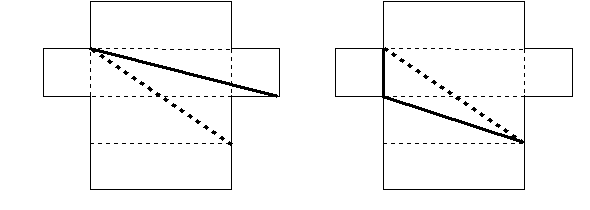
このように、立体を展開図にすれば平面上で考えやすいことがわかった。　

3　プロフィール

静岡県教育サークル　シリウス

1984年創立。
「理論より実践を語る」「子どもの事実で語る」「小さな事実から大きな結論を導かない」これがサークルの主な柱です。
最近では、技術だけではない理論の大切さも感じています。それは「子どもをよくみる」という誰もがしている当たり前のことでした。思想、信条関係なし。「子どもにとってより価値ある教師になりたい」という願いだけを共有しています。