変わり方調べ（小学4年算数）式・表・グラフの関係性まとめ！

本単元で身に付けたい資質・能力

本単元では、伴って変わる2つの数量の関係を式・表・グラフで表現し、相互に関連付けて考える能力を養う。また、身近な変化を数的に捉え、今後の生活や学習に活用しようとする態度を育む。

単元の評価基準

• 知識・技能：伴って変わる2つの数量の関係を式・表・グラフで表すことができる。
• 思考・判断・表現：伴って変わる2つの数量の関係について、式・表・グラフを用いて変化や対応の特徴を捉え、説明することができる。
• 主体的に取り組む態度：伴って変わる2つの数量の関係を、多面的に捉えようとする。

まとめ授業のポイント｜めくりドリルで起こすアクティブラーニング

まとめ授業の目標は以下の通り。

• 式・表・グラフの関係性を整理すること
  （グラフは直線で表せる場合のみ扱う。以下同様）

そのためには、ICTを用いた簡易計算ドリル（以下、「めくりドリル」と呼ぶ）を行うことが有効である。
めくりドリルとは、問題カード（⇒解説カード）⇒答えカード⇒問題カード⇒……（以下繰り返し）となるように並べたICT上の計算ドリルのことである。
本実践において活用するメリットは3つある。

1. 「問題文→式」以外にも、図等を用いて様々な出題形式のドリル演習が行える。
   例：「式→表」「表→グラフ」等
2. 個人またはペアで行うドリル演習なので、習熟度に合わせた個別最適な学習が行える。
3. 解説カードをヒントとして使うことで、苦手な児童にはスモールステップでの支援が可能。逆に、理解の進んでいる児童にはチャレンジ問題の出題が可能。

表やグラフをドリルに含めることで、式・表・グラフの相互のつながりを瞬時に確認できる。また、演習のペースを個人で設定ができるだけでなく、解説カードを活用することにより各自で難易度の調整ができるので、自然とアクティブラーニング型の授業となる。事前の準備にはやや時間がかかるものの、一度作れば次年度以降は簡単に使い回せるのも利点の1つだ。

まとめ授業の実践例｜式・表・グラフの関係性を理解

めくりドリルを活用した授業実践を示す。

提案するのは、めくりドリルを中心に据え、「理解したつもり」を「納得」に変えるアクティブラーニング型の授業実践である。

導入－振り返りと本時の目標設定

黒板にこれまでの学習で扱った式・表・グラフを提示し、それぞれの関係性を振り返る。

目標として、「式・表・グラフの関係性を整理する」という見通しを持たせる。

展開－めくりドリルを活用した多様な演習

めくりドリルを用いて「文章題→表」や「表→式」、「問題文→式」、「表→グラフ」等様々な形式での演習を行う。めくりドリルはいくつかの難易度に分けて作成し、以下のルールに沿って行うことを勧める。

1. 自分のレベルに合わせた難易度から始める。
2. めくりドリルが一つ終わったら、黒板にどこまで進んだかを書く。
3. ヒントカードや答えカードを見ても考え方が分からないときには、手をあげる。
4. チャレンジ問題（最難関の問題）が終わったら手をあげる。

これらのルールは、児童の学びを止めないこと、飽きさせないことを目的としている。長時間の演習になるからこそ、友だち同士が競い合いたくなるような仕掛けや立ち歩くことで異なる刺激を与え続けること等の飽きさせない工夫が必要だ。

また、めくりドリルを行っている時間、教員は基本的に手が空く。そのため、苦戦している児童のフォローや先に進んでいる児童の理解を深める問いかけが可能だ。

発展－式・表・グラフを用いて分かること

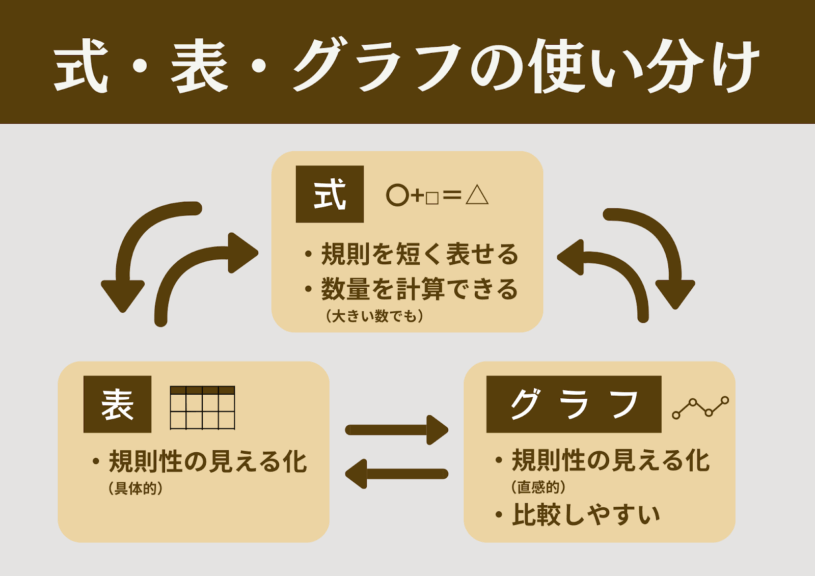
演習を通じて感じた式・表・グラフのそれぞれの特徴を話し合い、明確化する。

結論、特徴は以下の通りである。

• 式：規則を短く表せる、大きい数量でも計算できる
• 表：規則性に気づきやすくなる
• グラフ：数量の変化や関係を直感的に捉えられる、比較しやすくなる

以下のような具体例を用いて説明すると良い。

例えば「りんごの個数はみかん数より10個多い」という場面を考える。

式を活用するとき

「みかんが100個のとき、りんごはいくつか。」等、大きい数を扱う際には式に代入するのが最も早い。式は、長く書かれた問題場面を短く表しており、「りんごの数＝みかんの数+10」にみかんの数を入れるだけで、どれだけ大きい数でも計算すればりんごの数が求められる。

表を活用するとき

「みかんが1個、2個、3個・・・と増えたら、りんごの数はどうなるか。」等、数量の変化の規則性を見つける際には、表を用いるのが良い。

グラフを活用するとき

「『りんごの数がみかんの数の2倍のとき』と増え方はどう違うか。」等、変わり方を比べたいときには、グラフを用いるのが良い。

特に、いつ「2倍」の方が大きくなるのかなどが、グラフをかくことで直感的に捉えられる。

まとめ－関連性の整理と振り返り

「自分ならどのように、式・表・グラフを使い分けるか」を、自分の言葉でノートにまとめさせる。算数では答えを出すことばかりに目がいきがちだが、「目的に応じた使い分け」も同じくらい重要であることを意識させる。

執筆者

まき先生

中学高校で数学を教えている。体系的に教えるためには算数から学びなおす必要があると感じ、算数の授業案についても学習をすすめている。
実践的かつつながりを意識した授業案の作成に努める。