並べ方と組み合わせ方（小学6年算数）授業案｜順列と組み合わせの違いに気付かせよう

本単元で身に付けたい資質・能力

本単元では、順列や組み合わせについて、落ちや重なりのないように整理する方法を理解し、適切に数え上げることができる能力を養う。また、数学的表現を用いて考えた過程を振り返り、それらを今後の生活や学習に活用しようとする態度を育む。

単元の評価基準

• 知識・技能：順列や組み合わせについて、落ちや重なりのないように数え上げることができる。
• 思考・判断・表現：事象の特徴から、順列か組み合わせかを適切に判断し、落ちや重なりのないように図や表を用いて表すことができる。
• 主体的に取り組む態度：順列や組み合わせについて、数学的表現を用いて考えた過程を振り返り、それらを今後の生活や学習に活用しようとする

【授業案】順列と組み合わせの違いに気付かせよう

導入｜類似した場面を比較して、違いに気付く

導入では、日常的な場面をもとに「並べ方」と「組み合わせ方」の違いに気付かせる。

そのため、上画像の①・②を順に提示し、何通りの決め方があるかを考えさせる。問題場面を言葉にすると以下の通り。

①：A～Fの6人の中から、リレー選手を2人選び、走順を決めたい
②：A～Fの6人の中から、掃除当番を2人選びたい

導入の時間短縮のため、①の数え方を共有できたら②を提示し、同様の流れで考え方を共有させる。どちらの数え方も共有できたことを確認したのち、児童に「①と②のどちらの方が多くなると思うか」を問いかける。「どちらも同じ」との回答が多数あることが想定されるが、「①と②が異なる」という考えが出てきた場合にはそれを全体で共有して議論させたい。異なるという意見が出てこなかった場合は、②の画像において掃除の役割分担が明記された②’を提示し、「②と②’ではどちらが多いか」を問いかけ、②が既習の解き方では対応できないことに気付かせる。

展開｜順列と組み合わせの違いの言語化と演習

導入で用いた②と②’を用いて解き方の違いを丁寧に確認し、言語化する。

• 順列：選んだものの順番も大事
  （つまり、順番を考えない方が組み合わせ）

数え方まで確認した後、この考えをスモールステップで定着させるため、以下の順に演習を行う。

1. 比較して選ぶ
   同時に2つの問題場面（順列と組み合わせ）が提示され、組み合わせを選ぶ
2. 正誤判断をする
   問題場面が1つだけ提示され、順列なのか組み合わせなのかを答える。
3. 数え上げる

問題場面が1つだけ提示され、それを適切に数え上げる。

まとめ｜順列と組み合わせの違いの整理

まとめでは、順列と組み合わせの違いを自分の言葉で整理する。児童自身の言葉でまとめればよいが、言葉に詰まる児童もいるだろう。その場合には、「順列」「順番（順序）」という言葉は必ず使うよう指示すると良い。

【ポイント】違いに気付かせる工夫とは

導入での問題場面は画像で提示

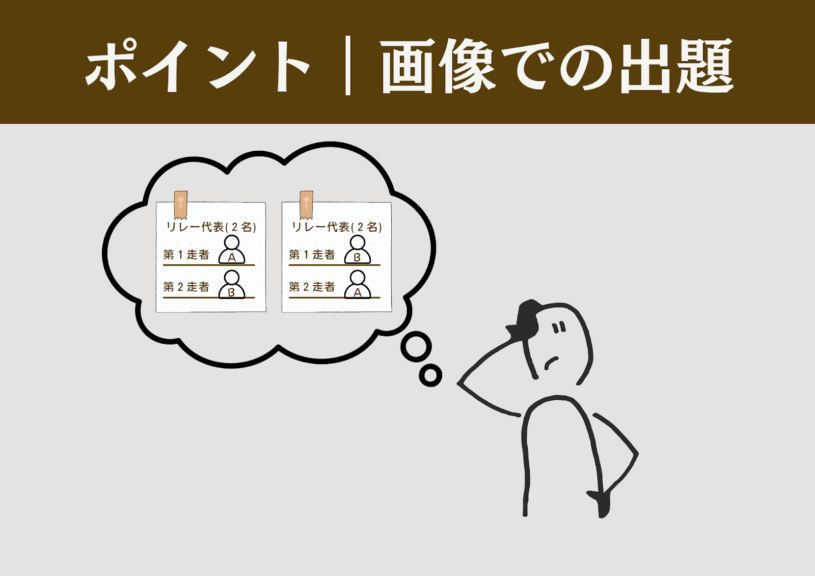
導入における問題場面の比較は、言語化せずに画像で提示することを推奨する。理由は、以下の2点である。

• 順列における「順番」や「並べ替え」は、日常使う言葉とニュアンスがやや異なる
  例：5人から級長と副級長を1人ずつ選ぶ（順番をつけたり、並び変えたりしない）
• 順列の問題では問題文の言い回したくさんあり、「言葉の暗記」では意味がない
  →実際に選んだり並ばせたりする場面を画像としてイメージできると良い。

順列と組み合わせの理解を深める3ステップ

順列と組み合わせの見極めは非常に難しい。理由は上述の通り、算数の用語と日常使う言葉とのニュアンスがやや異なるからだ。そこで、次の3つのステップで成長を促すことが有効と考えられる。

1. 比較して選ぶ
   類似した順列と組み合わせの場面を同時に提示することで、算数の用語である「順番」や「並べ替え」の意味を操作で理解できるようにする。
2. 正誤判断をする
   1で身に付けた算数の用語に対する理解を定着させる。
3. 数え上げる
   実際に問題が解けるようになる。

【発展】中学校への接続を考える

案1｜表での整理

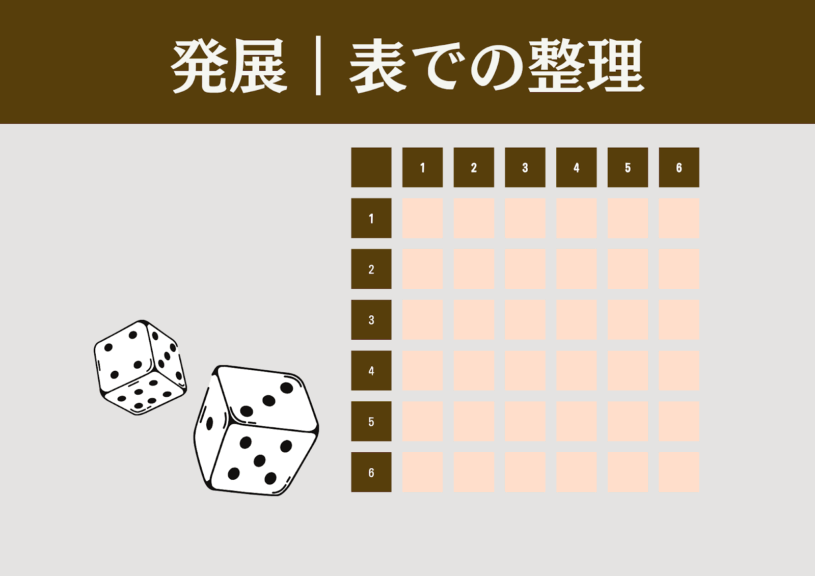
2個のさいころを題材とした問題を扱い、表を活用して解くと良い。さいころを2個使った問題は、中学校における確率の基礎につながる題材である。
導入に対するストレスが少なく、樹形図よりも数え忘れが起こりにくいのでお勧めだ。

【例題】大小2個のさいころを投げたとき、出た目の和が7になるのは何通りありますか。

区別の有無を入れると難易度が上がるため、基本的には区別のあるさいころのみを扱うと良い。

案2｜整数を作る発展問題

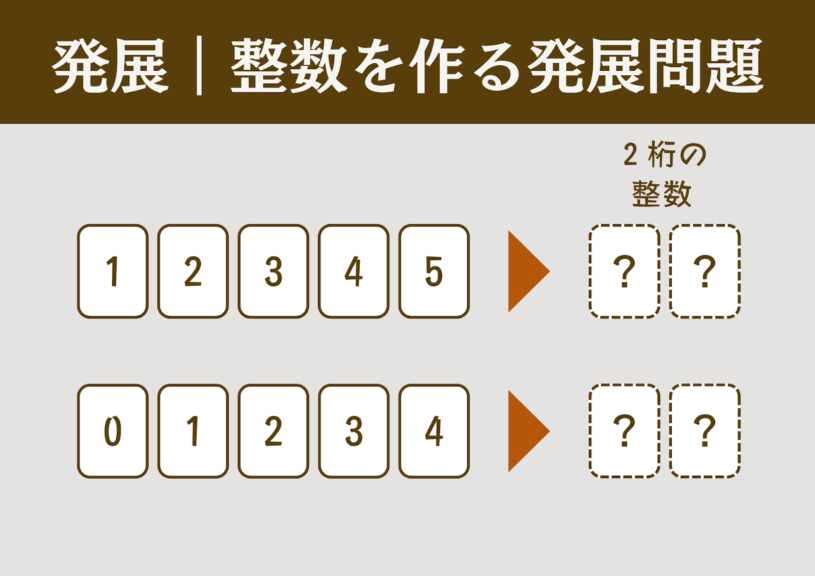
整数を作る問題は、少し工夫をするだけで簡単に、問題場面をきちんと想像しなければ解けない問題を作ることができる。

【例題】

1. 1から5までのカードが1枚ずつある。これらを使って2桁の整数を作る。
2. 1から5までのカードが1枚ずつある。これらを使って2桁の偶数を作る。
3. 0から4までのカードが1枚ずつある。これらを使って2桁の整数を作る。
4. 1から5までのカードが2枚ずつある。これらを使って3桁の偶数を作る。
5. 2桁の整数を作る。（重複有）

場合の数や確率では、実際の場面をイメージすることが何よりも重要なので、このような問題には少しでも触れられると良い。それぞれの問題で答えが異なる理由を考えさせるだけであれば、短い時間でこなすこともできるだろう。

執筆者

まき先生

中学高校で数学を教えている。体系的に教えるためには算数から学びなおす必要があると感じ、算数の授業案についても学習をすすめている。
実践的かつつながりを意識した授業案の作成に努める。