割合（小学5年算数）割合の存在に気づかせる授業案

本単元で身に付けたい資質・能力

本単元では、割合の基礎となる「くらべる量」「もとにする量」「割合」の関係性を理解し、適切に表現できる能力を養う。また、割合を用いた比べ方等を数学的表現を用いて考えた過程を振り返り、今後の生活や学習に活用しようとする態度を育む。

単元の評価基準

• 知識・技能：割合を用いて比べたり、割合を求めたりすることができる。
• 思考・判断・表現：割合を用いた比べ方や表し方を図や式などを用いて考え、表現することができる。
• 主体的に取り組む態度：図や式などを用いて考えた過程を振り返り、多面的に捉えて検討したり、生活に割合を活用しようとしたりしている。

授業実践｜くらべる量ともとにする量の見抜き方

導入｜「くらべる量」以外に注目する必要性に気付く

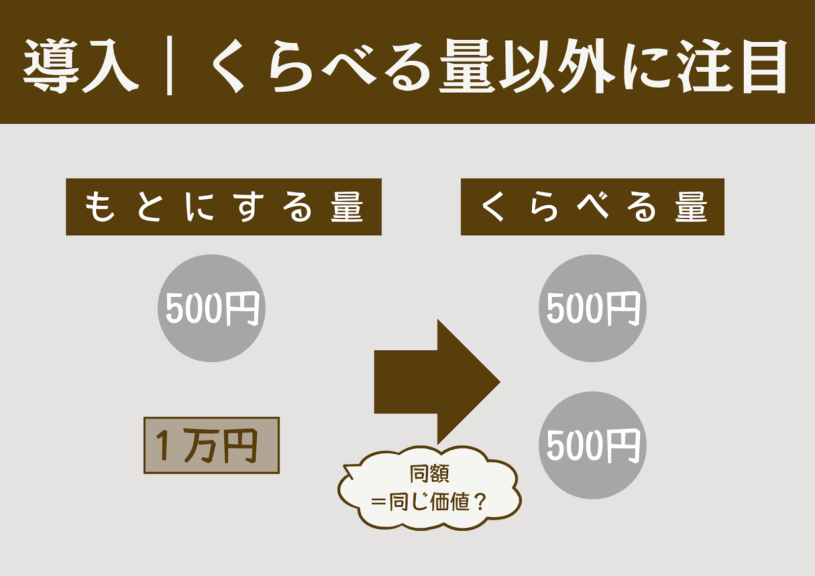
「お小遣いで500円もらったら、何に使う？」

開口一番、授業との関係が想像できない発問で児童の関心をひく。少なすぎる！　という声とともに、楽しげな発言が溢れるだろう。最高額を使う児童の意見は全体で共有し、その額を使うことに対する他の児童の感想を聞く。ここでは500円全額を使ったこととする。

「お年玉で合計1万円もらったら、何に使う？」

次の発問に移り、同様に発言を促す。当然買い物の額が大きくなっているだろう。この条件下で先ほど最高額であった「500円の買い物」をした場合の感想を聞き、同額の買い物にもかかわらず受ける印象が違うことを体感させる。

受ける印象が異なる理由を簡単に話し合わせ、「くらべる量」が等しくても、「もとにする量」が異なると適切な比較にならないことに気づかせる。
ここでは理解の深追いはせず、割合の存在に触れる程度に留める。

展開｜「割合」の存在に気付くためのグループワーク

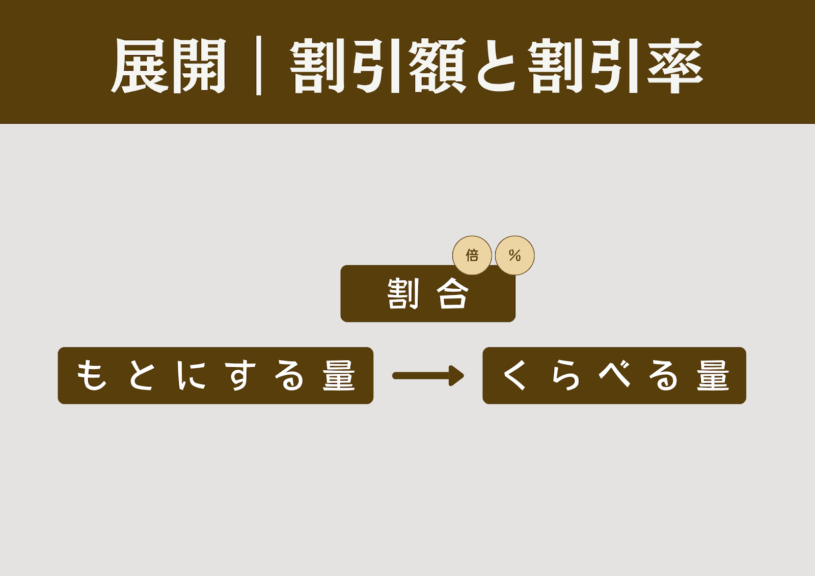
次に3つの商品のもとの値段、値引き額を順に示し、最もお得に買える商品はどれかを考えさせる。

商品	もとの値段	割引額
A	6000円	50円
B	300円	50円
C	100円	50円

児童が商品Aの割引率の小ささに注目できるよう、「特別に割引があります！」等割引額が大きいと思わせるような前振りをすると良い。導入時に「割引額」ではなく「割引率」に視点が切り替えられているので、商品Aの割引額に対して「少ない！」「ケチ！」という発言が得られるだろう。

ここで、「割引額が同じなのに『お得さ』が異なると感じるのはなぜか。また、どの程度の違いがあるのか。」についてグループワークを行う。もとの値段をすべて6000円に揃えることによって割引額を適切に比べられるようになるのだが、グループワークが難航した場合には以下の点をヒントにすると良い。

• どれが最もお得に感じられるのか。また、それはなぜか。
• 違和感はあるものの、なぜ適切に比べられないのか。また、それは改善できないか。

本実践では、「もとにする量」の重要性や「割合」の存在に気づくきっかけ作りを目標としているため、もとの値段が簡単にそろえられる値段設定にしている。理解度の高いクラスでは3つの最小公倍数をやや見つけにくい数にして、もう一段ハードルをあげても良いだろう。

まとめ｜「もとにする量」の重要性をまとめる

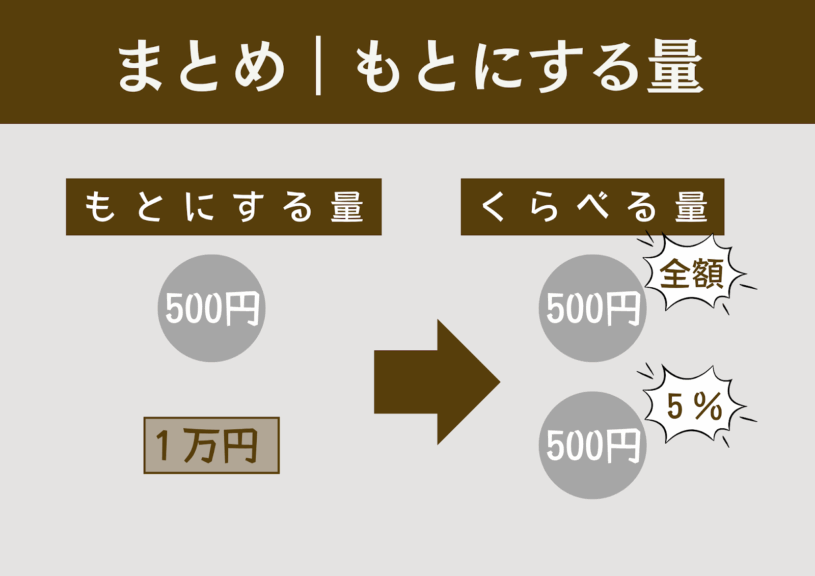
「もとにする量」が異なる場合、「くらべる量」を単純に比較しても意味がないこと、本時は「もとにする量」を揃えて適切な比較ができたことを再確認する。このやり方では、たくさんのデータを一度に比較するのは大変であることから、本単元で学ぶ「割合」の重要性を示し、次回以降の授業につなげる。

もし導入時に「先ほど全額の500円使ったのだから、今回も全額1万円使うべき」という割合に注目した意見が出ていたなら、「割合」の話につなげられると良い。

発展学習｜フェアトレードの仕組みに触れる「割合×SDGs」

発展学習の目的｜数の意味することを考えるきっかけ作り

本実践では、題材の設定を「お金」に限定している。それは、児童のもっとも身近なものであり、フェアトレード等の社会課題につながるからである。

残念ながら算数では、登場人物がどれだけ速く走っても、どれだけ高得点をとっても、数値としてしか認識されず賞賛されることはない。それは日常の買い物でも同様で、同じ商品であればお得かという基準でしか選択されず、その商品が作られる過程や背景を意識することはあまりないだろう。本発展学習を単元の最後に行い、算数を数字遊びでは終わらせず、その奥に潜む真実に目を向けられるきっかけづくりとなることを願う。

発展学習の概要｜買い手と売り手に分かれて感想を共有する

売り手と買い手に分かれて1つの商品の売買を行うゲームをする。ルールは以下の通り。

• 児童はグループごとに2名の売り手と4名程度の買い手に分かれる。
• 売り手には「原価」と「定価」、買い手には「定価」と「売値」が示されている。
• 制限時間は3分
• 買い手の所持金は全員一律
• 売り手は利益が最も多い人の勝ち。
• 買い手は最も多く商品を購入できた人の勝ち。
• 売り手は「割合でのみ」割引をしても良い。（●円引きは×）

売り手は同じ商品なので、買ってもらうためには値引きが必要となる。しかし値引きをしすぎると赤字になってしまうため、売値は原価に収束していくだろう。

最後に売り手と買い手の感想を共有し、割合が生活に生きる重要な道具であることを学ぶとともに、フェアトレードの大切さと難しさを体感する機会とする。

執筆者

まき先生

中学高校で数学を教えている。体系的に教えるためには算数から学びなおす必要があると感じ、算数の授業案についても学習をすすめている。
実践的かつつながりを意識した授業案の作成に努める。