本単元で身に付けたい資質・能力
本単元では、身近にある箱の形をしたものを観察したり作ったりする活動を通じて、図形を構成する要素に着目してとらえる力を養う。また、それらを今後の学習に活用しようとする態度を育む。
単元の評価基準
- 知識・技能:「はこの形」をしたものの構成要素を理解し、辺や面を組み合わせて箱の形を構成することができる。
- 思考・判断・表現:面や辺、頂点などの構成要素に着目し、「はこの形」の特徴を見出し、説明することができる。
- 主体的に取り組む態度:身の回りにあるものの形から「はこの形」をしたものを見つけ、特徴を捉えようとする。
ゲームで学ぶのが有効な理由
「はこの形」は、立方体と直方体の構成要素(面・辺・頂点)や展開図について学ぶ単元である。
知識として理解するのは容易だが、一方で、頭の中で適切な立体を思い描くことができない児童は多い。例えば、辺や面の関係性が理解できておらず、ねじれの関係にある辺を伸ばしたら交わると思っていたり、立体を見て、隠れている部分を適切に想像できなかったりする。
この単元では、体験を通して空間的に考える力を育てることが重要である。
そこで有効なのが「ゲーム学習」である。ルールの中で試行錯誤し、想像と具体物の操作を相互に行う過程で、自然と空間への理解が深まる。
ゲーム①|「はこの形」はどっち?
「『はこの形』はどっち」のゲーム概要
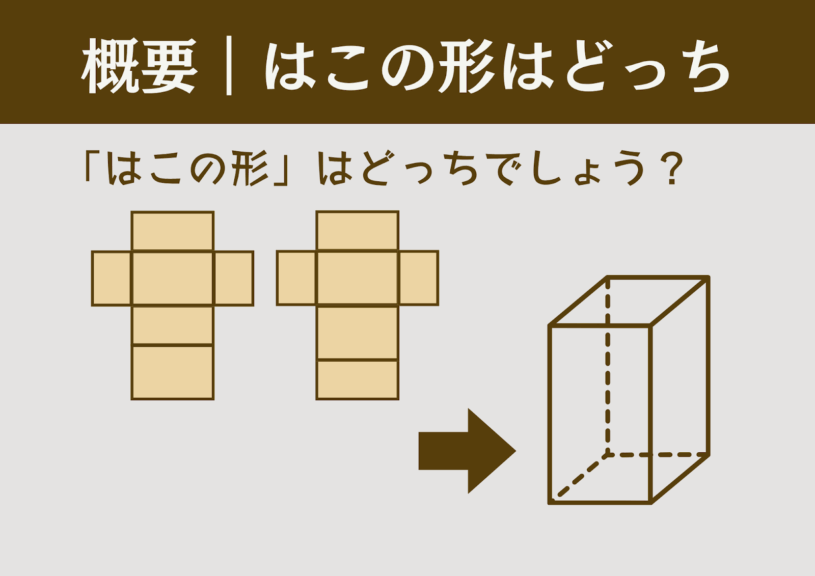
2種類の似た展開図を提示し、「はこの形(立方体または直方体)」になるのはどちらかを当てるゲーム。
一見よく似ているが、組み立てると片方は「はこの形」にならない図が含まれている。児童は頭の中で展開図を組み立て回答し、実際に展開図を組み立てて答え合わせをする。
グループワークにすることでアクティブラーニング型の授業となり、想像力をより強化できる。
このゲームは平面から立体を想像するので、「はこの形」の面や辺の関係性をとらえるのに優れたワークである。
「『はこの形』はどっち」実践の流れ
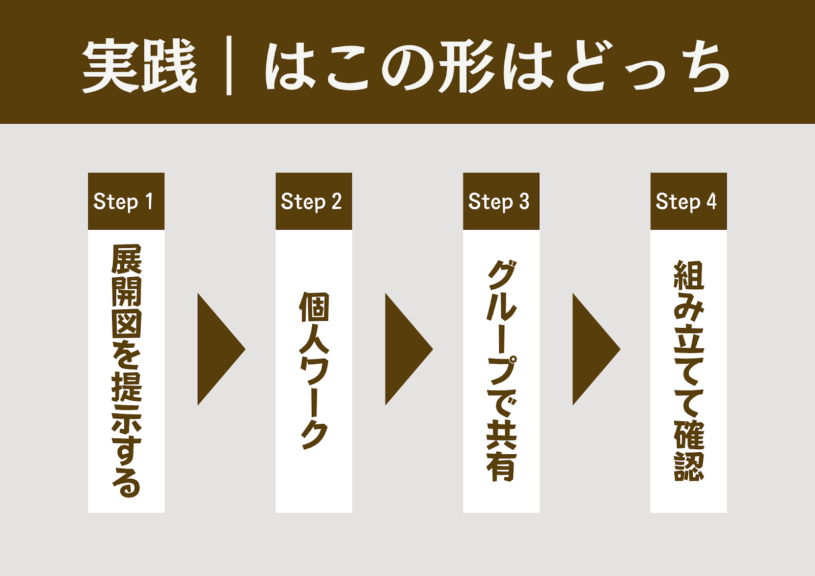
- 展開図を提示する
2種類の展開図を同時に提示する。
例:直方体の展開図と、面を入れ替えて合同な長方形の面が向かい合わない展開図 - 個人で考える(1分)
どちらが正しい「はこの形」なのか、理由も含めて考える。 - グループで話し合う(3分)
個人で考えたことを共有する。
反対意見が出たときは、グループですり合わせを行う。 - 実際に組み立てて確認(3分)
実際に展開図を組み立てて、答え合わせをする。
この際、「はこの形」を作れなかった理由を言語化する。
「『はこの形』はどっち」のポイント

- 空間イメージの形成
想像し、グループワークでその想像を強化し、実際の操作で確認をすることで空間的思考力が育つ。 - 誤りから学ぶ視点
間違った展開図を使うことで、抽象的な考えを言語化する補助をする。
ゲーム②|大きなさいころを作ろう!
「大きなさいころを作ろう!」のゲーム概要
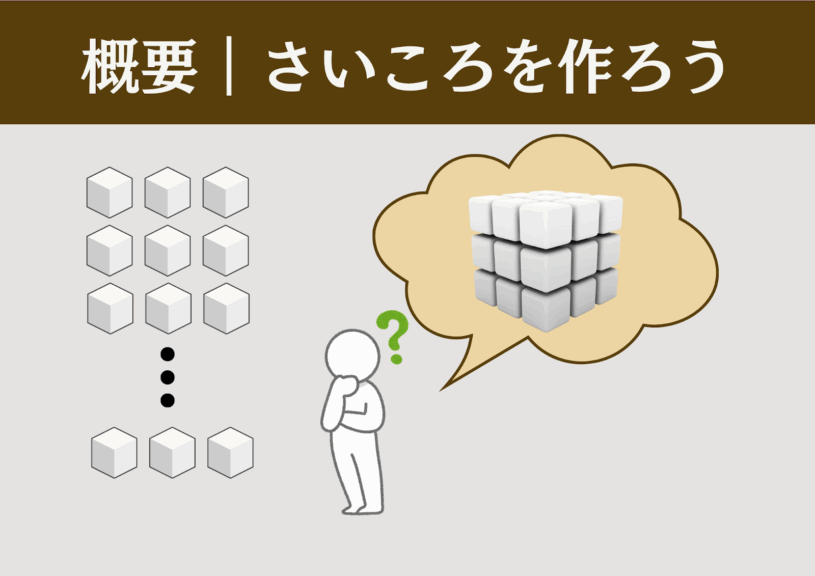
同じ大きさの小さなさいころ(立方体)を指定された個数すべてを組み合わせて、大きなさいころ(立方体)を作ることができるかを考えるゲーム。
児童は、指定された数から、大きなさいころを構成できるかどうかを考えて回答し、実際に作って答え合わせをする。
グループワークにすることでアクティブラーニング型の授業となり、想像力をより強化できる。
このゲームは立体を積み重ねて立体を作るので、「はこの形」の正面からは見えない部分を適切にとらえるのに優れたワークである。
「大きなさいころを作ろう!」実践の流れ
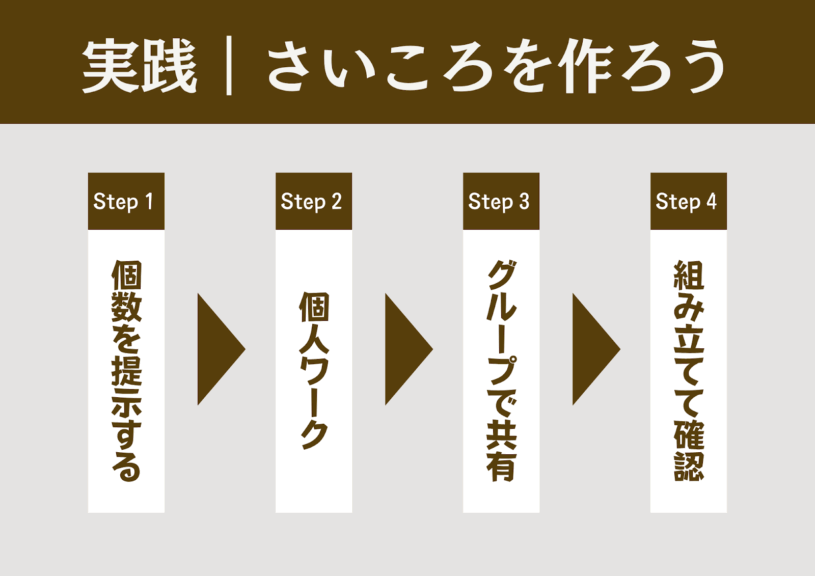
- 問題を提示する
同じ大きさの小さいさいころの数を指定し、すべて使って大きなさいころが作れるかを問いかける。
(例:15個・20個・27個など) - 個人で考える(2分)
児童は頭の中でどのように積むかをイメージし、さいころを作れるかどうかを判断する。このとき勘で回答されないよう、さいころを操作することは禁止するが、図などを用いて考えることは許可する。 - グループで話し合う(3分)
個人で考えたことを共有する。
反対意見が出たときは、グループですり合わせを行う。 - 実際に作って確認(3分)
実際に組み立てて、答え合わせをする。
この際、正面から見えない部分が思い描いた通りだったかどうかを確認する。
「大きなさいころを作ろう!」のポイント

- 空間イメージの形成
想像し、グループワークでその想像を強化し、実際の操作で確認をすることで空間的思考力が育つ。特に、目に見えない部分の想像、大きなさいころが作れなかったときの不足部分の想像をし、適切に言語化する流れが重要。 - 発展的な学び
「1~100までの間で、大きなさいころが作れる個数はいくつあるか」を考えさせることで、立体の体積と1辺の長さ(小さい立方体の個数)の関係に気付くきっかけを与えられる。
執筆者
まき先生
中学高校で数学を教えている。体系的に教えるためには算数から学びなおす必要があると感じ、算数の授業案についても学習をすすめている。
実践的かつつながりを意識した授業案の作成に努める。









コメント