分数のたし算とひき算（小学5年算数）通分と約分の授業案

本単元で身に付けたい資質・能力

本単元では、分母の異なる分数を通分して計算できる能力を養う。また、約分により分数を整理し、日常の数量の比較や表現に活用しようとする態度を育む。

単元の評価基準

• 知識・技能：約分や通分、異分母の分数の加減計算ができる。
• 思考・判断・表現：単位分数に着目して、異分母の分数の比較や加減計算の仕方を説明することができる。
• 主体的に取り組む態度：通分や約分の意味、異分母の分数の加減計算の仕方を考える過程を振り返り、多面的に捉えて検討しようとする。

分数の通分と約分の授業ポイント

小学4年生までの既習事項を土台にする

児童は小学4年生の授業「同値分数」にて、以下のことを理解している。

• 分母が同じであれば分数の大小を比較しやすい（≒計算しやすい）こと
  例）⅖と⅘
• 分母が異なれば比較しにくいが同値分数を活用すると比較しやすくなること
  例）⅖と⅓

同値分数の授業案：URL

上記URLの授業案のように、「分母と分子に同じ数をかけると同値分数が見つかること」を把握していると、通分の授業は非常にスムーズに進むだろう。小学4年生の段階では、規則としてそうなることを把握している程度であり、理屈は下記1時間目の授業で丁寧に取り扱う必要がある。

「めくりドリル」で起こすアクティブラーニング

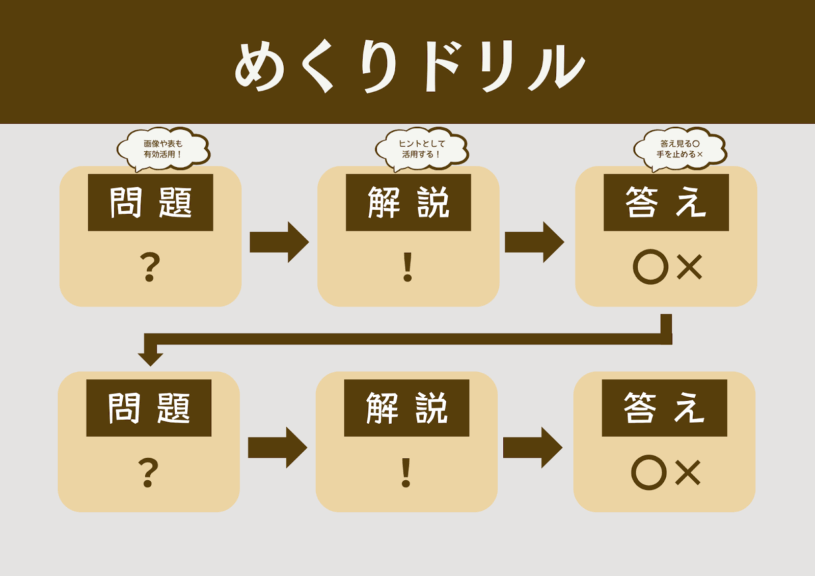
約分や通分は、理屈を理解したからすぐにできるようになるものではなく、演習をこなして慣れることが重要である。そのためには、ICTを用いた簡易計算ドリル（以下、「めくりドリル」と呼ぶ）を行うことが有効である。
めくりドリルとは、問題カード（⇒解説カード）⇒答えカード⇒問題カード⇒……（以下繰り返し）となるように並べたICT上の計算ドリルのことである。
本実践において活用するメリットは2つある。

1. 1問ずつ正解不正解を判断しながら進んでいけるので、非常に効率が良い。
2. スピード感や進捗を肌で感じられ、単調な演習も楽しんで行える。

演習のペースを個人で設定ができるだけでなく、解説カードを活用することにより各自で難易度の調整ができるので、自然とアクティブラーニング型の授業となる。本実践では解説カードにものさしの図をいれると、分母分子を等倍することの意味が少しずつ理解できるようになってくるだろう。事前の準備にはやや時間がかかるが、一度作れば次年度以降は簡単に使い回せるのも利点の1つだ。

1時間目｜通分の基本をとらえる授業案

異分母でも分母をそろえられることの復習

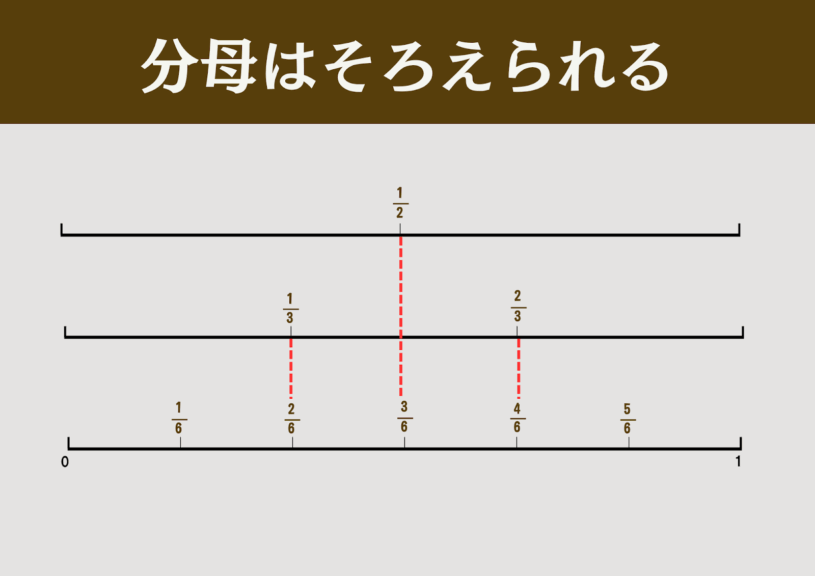
2つの分数を提示し、どちらが大きいかを考える活動を何度か行う。基本は同分母の分数を扱い、最後のみ異分母の分数を提示する。

例）⅕と⅗→7/3と2⅔→½と⅓

小学4年生「同値分数」で示した数直線を用いて、異分母でも分母をそろえられることを復習する。

分母・分子に同じ数をかけても値は変わらないことを確認

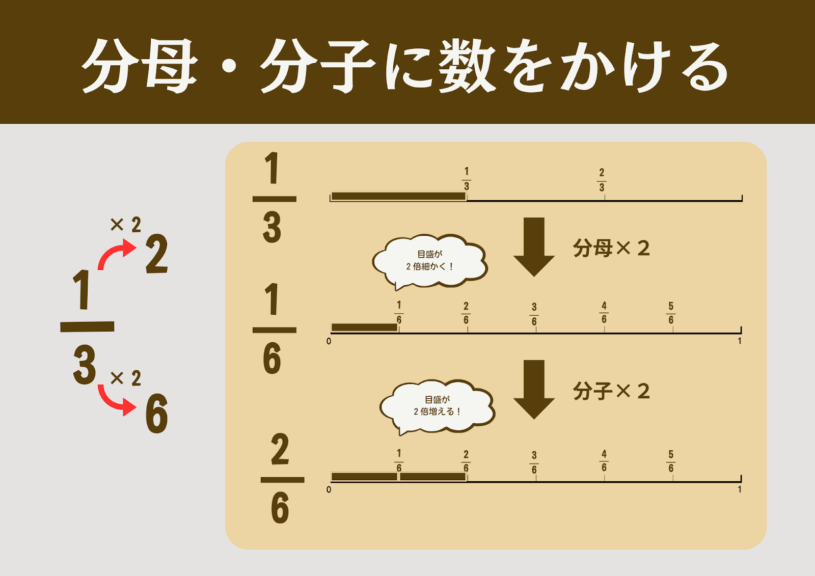
分母・分子に同じ数をかけたら同値分数が見つかる理屈を掘り下げる。前提として、分数の積や商は習っていないので、分母と分子の意味付けに基づいて丁寧に説明することが必要である。

分母・分子の意味付けは以下の通りである。

• 分母：ものさしの目盛を表した数
  分母が大きい＝目盛が細かい、分母が小さい＝目盛が粗い
• 分子：何目盛分かを表した数

「分母に数をかける＝目盛がより細かくなる」であり、「分子に数をかける＝何目盛あるかが増える」ということが分かれば良い。

簡単な通分2パターンにおける加減計算に挑戦！

めくりドリルを活用して、以下の通分2パターンにおける加減計算に挑戦する。

• 約分が絡まない、片方の分母がもう片方の最小公倍数になっているパターン
  例）½+⅛
• 約分が絡まない、分母最小公倍数が容易に想像できるパターン
  例）½+⅓

まだ分母を最小公倍数とするべきことや約分についての学習はしていないが、ここで簡単な通分の加減計算を扱った方が良い。

理由は以下の2点である。

• スモールステップで成功体験が積める。
• 分母を最小公倍数としない回答を提示することにより、次回以降の授業へのつなぎとなる。
  例）½+⅓＝6/12+4/12＝10/12

児童に間違えさせてはいけないと、丁寧に教え込んでからしか演習をしない教員がいる。その想いも素敵だが、今の知識では解決できない問題に直面し、それが次の学びへの原動力となることもあるのだ。

2時間目｜約分を理解する授業案

分母・分子を同じ数で割っても値が変わらないことを確認

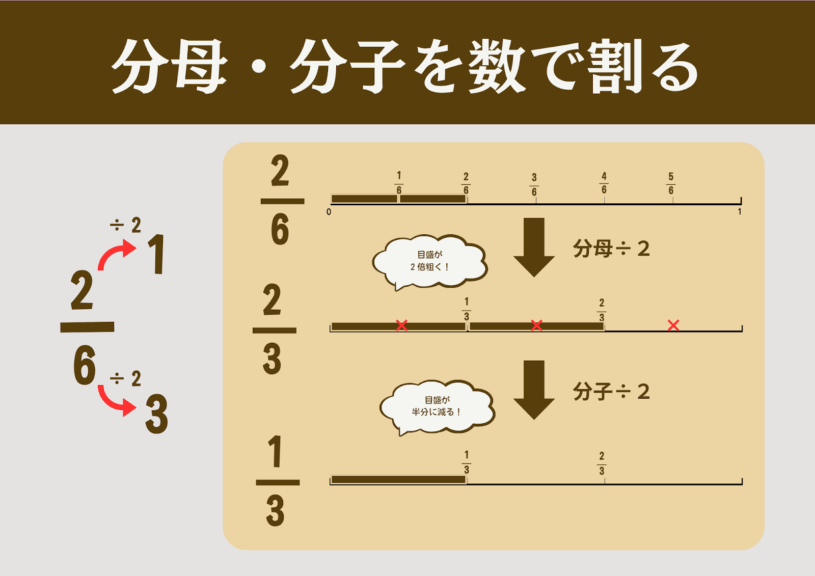
分母・分子を同じ数で割っても値が変わらないことを、通分と同様に示す。

その後、めくりドリルを活用して、以下の手順で演習を行う。

1. 約分のみ
   例）2/6＝⅓、8/12＝⅔等
2. 加減計算のあとに約分
   例）½+⅙＝4/6＝⅔
3. 約分のあとに加減計算
   例）2/6+4/3＝⅓+4/3＝5/3
4. 約分のあとに加減計算をして約分
   例）2/6+⅔＝⅓+⅔＝3/3＝1

合言葉「約分は、かさと一緒」で習慣化

約分を忘れる児童は非常に多いため、合言葉「約分は、かさと一緒」を用いて思い出せる工夫をしておくと良いだろう。傘をさすかどうかを毎日の登下校時に天気予報や雲の様子で判断しているように、約分するかどうかを毎回分数を見るたびに判断する必要がある。分数を扱う際には「傘持った？」と聞き、児童に必要の有無を回答させるくらい徹底すると良い。

執筆者

まき先生

中学高校で数学を教えている。体系的に教えるためには算数から学びなおす必要があると感じ、算数の授業案についても学習をすすめている。
実践的かつつながりを意識した授業案の作成に努める。