1 概要
この実践は(株)教育同人社の許可を得て、「はなまるサポート」の学習指導ポイント一覧より転載しています。
実践の続き(無料)は下部のURLからご覧ください。
また、以下より実践をPDFでダウンロードできます。
添付ファイル
2 この単元を取り扱うにあたって
4年生で、まだ長方形の求積公式が未習の子どもたちのほとんどが「えっ?面積?たて×よこでしょ!」と言うという話を聞いたことがあります。子どもによって、あるいは地域によって、未習であるはずの事柄が未習でない場合がよくあります。
しかし「なぜ?」を連発すると、ほとんどの子どもが白旗を揚げてしまいます。聞いて覚えたり、機械的に覚えたりすることが多いのですね。私たち教師の仕事は、その「なぜ?」に答えられる子どもを育てていくことです。
(初等教育研究所 山﨑 憲)
3 はじめに
「広さ」と「面積」という言葉について
通常「広さのことを面積と言います。」と定義していることが多いのですが、少し考えてみましょう。
「広さ」は、広い、狭いと言います。ところが「面積」は、大きい、小さいと言います。ここに違いがあると言えば確かにそうですね。広い、狭いは幅(長さ)を表すこともありますが、囲まれた地域全体というイメージでしょう。それに対して大きい、小さいは、明らかに数値です。そう考えると、「面積は数値で広さを表したもの」という見方もできます。
つまり、広さ比べを数値で行う、そこに「面積」が登場するという考え方です。4年生では広さを数値化します。はじめは「任意単位」による数値化(1年の大きさ比べでも扱う)、任意単位の不都合から普遍単位の導入と進みます。そう考えると導入に当たっては「広さを数で表そう」という目当てができそうです。
4 面積とは何かを考える。
普遍単位の導入と求積
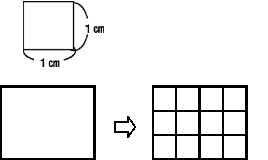
共通の面積の単位として1cmを教えます。そして、身の回りの広さを数値で表す、つまり「面積」を1cmのいくつ分かで表すことにします。
そうすると、基本的な図形の面積は、通常1㎝のメモリで区切る必要が生まれます。よく、はじめから方眼上に図形が描かれているものを見かけますが、本来は自分で1㎝のメモリをつけて区切るのです。そのことによって、「今、自分がしていることは、1cmがいくつあるかを知るためにしている作業なんだ。」ということを自覚します。それが明確な目的をもった算数的活動です。
1cmのいくつ分かを求める手順
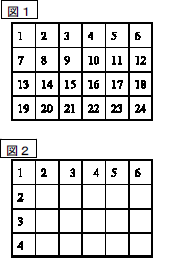
例えば図1のように、長方形を1cmのますに区切ってそれがいくつあるかを求める場合、1つずつ数えていく方法があります。しかし、これはあまりうまい方法とは言えません。ますの数が多くなれば数えるのが大変だという意見が出るようにしたいです。そこで「数えるのに,何かもっとうまい方法はないか」と問うのです。
図2のように、「たてに4こ、横に6こ並んでいるから、全体のますの数は、4×6で求められる」と考える子どもがいてよいのです。この子はかけ算の意味をよく理解しているとみることができます。
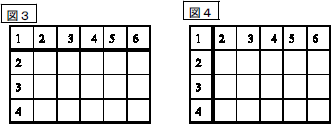
また、図3、図4のように横の4段分、たての6列分とみる見方も価値ある見方です。図2と同様にかけ算の意味理解ができている子どもたちですから、このようなアイディアはしっかり価値付けしてあげる必要があります。
ここまでの考え方は、教師が教えることではなく、子どもたちが自らの力で見出すことができる内容です。
5 面積の求め方を考える。
求積公式の理解
このように、図2、3、4などによって1cmの個数をうまく算出する方法が見つかったのです。つまり1cmの個数は、4×6や6×4の式で求められることに気づいたのです。
では、この式の「4」や「6」はそれぞれもともと何を表していた数だったのでしょうか。
「4」は【長方形のたての長さを表す数】、「6」は【長方形のよこの長さを表す数】でした。
つまり、4×6の意味は、
(長方形のたての長さを表す数)×(長方形のよこの長さを表す数)
ということです。
長方形の面積(たての長さを表す数)×(よこの長さを表す数)
長方形の面積(たて)×(よこ)
というように省略した言い方であり、「長さ」×「長さ」ではないのです。
求積公式のさらなる理解のために
長方形の求積公式 長方形の面積=(たて)×(よこ) の理解は、その公式の成り立ちだけで確かめるのでは不十分です。それは、この長方形の面積は何によって決まるのか、その依存関係を明らかにすることです。
つまり、長方形の面積は、たての長さと横の長さがわかることによって決まることを確認しなければなりません。
そこで求積公式を活用して、いろいろな要素を含んだ複合図形の求め方を考えます。
求積公式を活用した、複合図形の問題とその指導に関しては、以下のURLからご覧になることができます。この実践の続きには、東京都算数教育研究会発表会に提案された実際の問題も含んでおります。
http://www.djn.co.jp/support/special/point/docs/2011/11/2/1.php
また、概要から実践をダウンロードすることもできますので、ぜひご利用ください。
6 実践者紹介
山﨑 憲
元東京都算数教育研究会会長。
「小学校時代から現在までで,今が最も算数がすき」と,小学校退職後も算数教育に没頭し,現職時代に引き続き年に数回研究授業も試みている。
現在東京学芸大学講師として初等算数科教育法を担当。
またボランティアとして東村山市算数教室を開催し算数好きの子どもの育成を目指している。
7 サービス紹介
同社の「はなまるサポート」では、若い先生のための授業ヒント集として、毎月の学習指導ポイントを細かく解説しています。また、不明点や疑問点などを無料で相談を受け付けています。
http://www.djn.co.jp/support/
(編集・文責:EDUPEDIA編集部 佐藤 睦)









コメント