1 はじめに
算数や数学で、授業の前半に「基礎の課題(共有の課題)」をやって、授業の後半に「ジャンプの課題」をグループ学習でやります、という「本時の展開」の流れを、よく耳にします。
2 「円の面積」
小学校6年生の算数「円の面積」の場合、次のような「基礎の課題(共有の課題)」と「ジャンプの課題」を提示した授業があったことを、教えてもらいました。
ポイントだけ、かいつまんで、教えてもらったので、細かいところまでは、わかりません。
3 本時の展開(概要)
本時の概要だけです。(あわててノートにメモしたことだけ)
まず、「共有の課題」は、「円の面積」の公式です。
つまり、半径×半径×円周率=円の面積、ということになります。
ジャンプの課題
そして、「ジャンプの課題」は、「下図の斜線部の面積を求めよう」です。
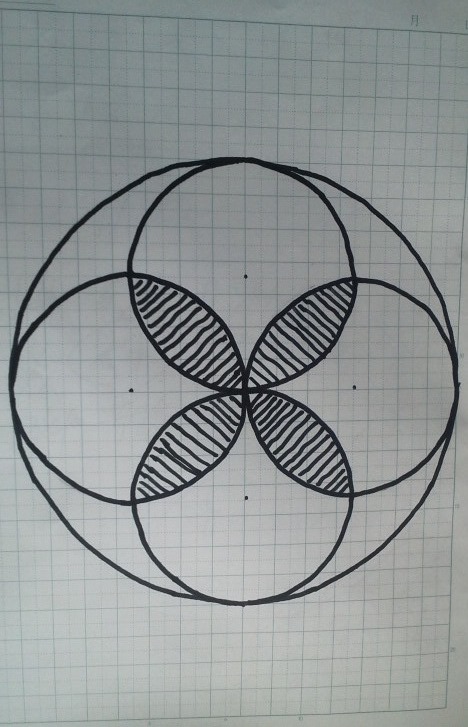
コンパスで大円1つと小円4つを書いてから、サインペン(フリーハンド)でなぞりました。
フリーハンドで、すみません。
点はコンパスの跡(小円の中心)です。
教えた数字は、大円の半径の長さだけ。(小円の半径が計算しやすい数字8cmや10cm)
グループ学習(男女混合4人班)
この「ジャンプの課題」について、子どもたちは、4人グループ(男女混合班)で、あれこれ話し合いながら解いていったそうです。
私は、円の面積の公式を使って計算できるようになったばかりの段階で、こんな応用問題が解けるのだろうか?と思いました。だからこそ、グループ学習による「ジャンプの課題」として、採り入れる価値があるという説明を受けました。
子どもたちは、円の面積の公式以外に、それまでに学んでいる、三角形の面積の公式も使ったそうです。
大円の半径が、小円の直径であることは、すぐに気づいたとのことです。
各グループで、4人の知恵をしぼって見事に解いていったと、伺いました。
小学校6年生の先生方、もし、時間的余裕があれば、この「ジャンプの課題」のグループ学習にチャレンジなさってみては、いかがでしょう。









コメント