はじめに
第61回読売教育賞を受賞した見目宗弘先生の実践です。
説明文の主題をより説得力のあるものにするために用いられる具体例。その取捨選択がどのように行われるかを児童に教え、作文を書くときに活用できるようにするための指導案になっています。
この記事では具体例選択の考え方を学術的に説明してそれを児童に教えるための実践を、次の記事ではその考え方を作文で使えるようにさせるための実践を紹介します。
説明文の具体例を選択する方法を教える(2)(見目宗弘先生)… http://p.tl/61mq
帰納推論について
説明文と帰納の関係
説明文の「はじめ」「なか」「おわり」という構成の「なか」の部分には具体例が配置される。その「なか」の具体例はどのように選択されるのだろうか。複数ある具体例の中からある具体例が選択される、その選択の理由は何か。
具体例は何らかの結論、あるいは主張を示すために選択される。選択の理由の考察には、具体例と結論の結びつきを押さえることが必要となる。
市毛勝雄氏は、説明文の構成を説明している中で、その両者の結び付きについて、次のように述べている。
まとめ(中略)…具体例(中略)に共通している「よく働く」という性質を取り出して述べる部分である。これはいわゆる帰納という思考法である。
つまり、帰納に関する知見を整理すれば、具体例を選択する理由が得られるはずである。
「確からしさ」について
帰納とは「いくつかの具体的な観察事例から一般的帰結を導く機能的一般化」であり、次のような特徴を持つとされている。
何らかの経験や情報から、意味情報を増加させるような(従って真であることが保証されない)結論を導く蓋然的(がいぜんてき)推論全般を指して用いられることが多い。}
この特徴は吉住チカ氏が挙げている例からも確認することができる。
- パガニーニは指が長い。
- ラフマニノフは指が長い。
- リストは指が長い。
- →すべての演奏技術に長けた作曲家は指が長い。
住吉氏の結論は、未知のことをも推測して述べている新しい情報である。だが、その結論は正しいとは限らない。
このように、帰納は「結論の“もっともらしい(可能性が高い)”あるいは“有り得そうにない(可能性が低い)”という確からしさ」で測られる。認知心理学ではこの確からしさを「確証度」「確信度」というが、本稿では、認知心理学の知見を教育の場において活用するため、以後「確からしさ」という用語を用いる。
「前提」について
その「確からしさ」に影響を与えるのが前提である。市川伸一氏はそのことについて次のように説明している。
帰納的推論においては、前提(あるいは「データ」といってもよい)がどれくらい結論を支持するかという「程度」があるのだ。
引用中の前提とは、説明文で用いられる具体例や日常的に用いられる「前例となる事実やここの場合におけるそれぞれの事実」という意味の事例と同義ではない。前提は、論証構造の中に位置づけられるからだ。
だが、「前提には結論を支持する『程度』がある」という知見は、説明文の具体例を選択するとき、選択の基準の一つとして活かすことができるだろう。
(以下、用いる「事例」という語は論証構造の中に位置づく「前提としての事例」である。日常的な意味の「事例」とは異なるものである。)
「カテゴリに基づく帰納推論」について
住吉氏は先に挙げた例をもとに「(前略)前提に挙げられているのは、パガニーニ、ヘンデルなど特定の人間であり、現実世界に唯一の事例である」と述べ、「このような事例を個体という」と説明している。
そして、「これに対して、前提にそれら個体の集合、つまりカテゴリを挙げているような論証を考えてみよう」といい、次の例を挙げる。
- トランペッターは指が長い。
- フルーティストは指が長い。
- →すべての器楽奏者は指が長い。
この事例のトランペッターはトランペッターたちであり、フルーティストはフルーティストたちである。また、結論の器楽奏者も器楽奏者たちを表した集合体である。住吉氏は「このような帰納論証で表される推論を、カテゴリに基づく帰納推論と呼ぶ。」と説明する。
「カテゴリに基づく帰納推論」は、「(前略)結論は前提カテゴリの上位カテゴリである。」という特徴を持つ。つまり、次の図のように事例と結論の関係を「集合」で考えることができるのである。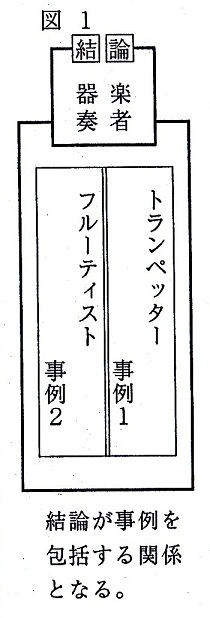
この「カテゴリに基づく帰納推論」において事例が結論に与える心理効果を、オシャーソンたちは次のようにまとめた。
- 典型性:前提事例が典型的であるほど、結論への確信度は高くなる。
- 単調性:前提事例が多いほど、結論への確信度は高くなる。
- 多様性:前提事例が多様なほど、結論への確信度は高くなる。
- 均質性:結論カテゴリーが均質であるほど、結論への確信度は高くなる。
- 非単調性:前提事例に不適切な事例が加わると、結論への確信度は低くなる。
この知見は説明文の具体例選択の基準になり得るものであろう。
具体例選択の方法を児童に教える
5つの知見を教える
前提となる事例が結論に与える影響を児童に教えることで、児童は結論を確かなものにするための具体例を選択することができるようになるだろう。
住吉氏がすでに事例に関するもの(「典型性」「単調性」「多様性」「非単調性」)を児童が理解することができるという検証を行っており、結論に関する知見(「均質性」)も小学4年生は理解可能と考えたので、これら5つの知見を小学4年生に教えた。
授業では、次の問いに答えさせ、一問ずつ教員が説明をするという形で選択の基準を教えていった。なお、オシャーソンたちが用いた問いでは児童には難しいと思われたため、問いは教員が作成した。
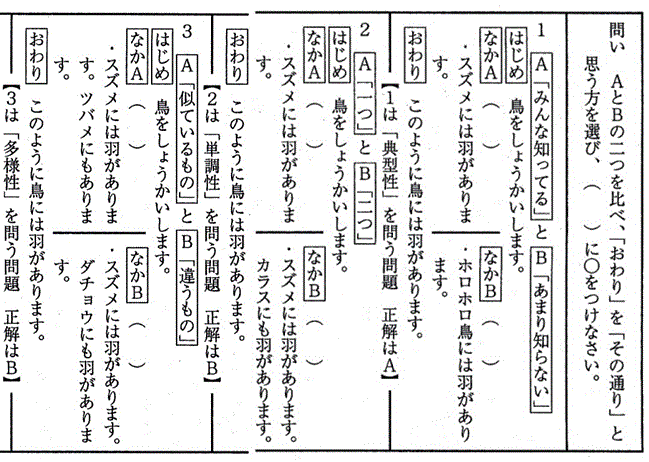
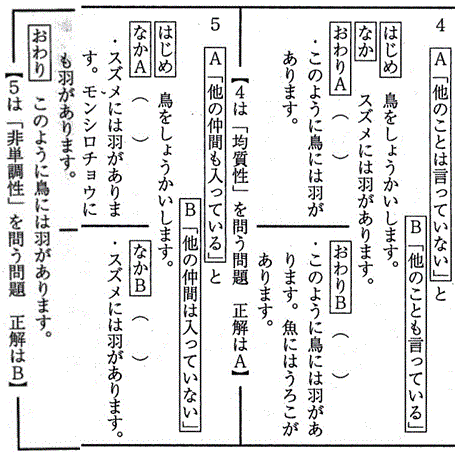
児童には次の説明を行った。
問いの解答をすると、多様性の問題以外はほとんどの児童が正解した。
「多様性」を教える
「多様性」に基づく選択では、「スズメとツバメ」と「スズメとダチョウ」とをどう比べていいのか分からず、児童はつまずいていた。「小さい鳥どうしを選ぶよりも小さい鳥と大きい鳥を選んだほうがいろいろな鳥になる。そのほうが、どんな鳥も羽を持っていると思われる」と説明したが、その仲間分けの仕方がわかりにくいようだった。
「多様性」に基づく選択の問題には、住吉氏がオシャーソンたちの研究を検証する際に懸念していたことがあった。「『多様である』と判断するその尺度が恣意的になってしまう」という点だ。そのため、多様である選択を、「結論に内包される別々の仲間から事例を一つずつ組み合わせて選ぶこと」と考えた。
このことを踏まえ、「多様性」を理解させるために次の問題を解かせた。問題は1から3まで全て解かせた後に解答した。また、解答の際には、下の図を黒板に書き、違う仲間の選択が視覚的に分かるようにした。

問1は、「遊び」の仲間から選択できればよい。「上手な選択」として次の説明をした。
「校庭の遊び」と「室内の遊び」から1つずつ選ぶと「いろいろな楽しさ」を説明できる。
問2は「やるべきこと」の仲間から選択できればよい。「上手な選択」として次の説明をした。
「やらなくてはならない仕事」と「やっておいたほうがいいこと(任意)」から1つずつ選ぶと、「いろいろなやるべきこと」を説明できる。
問3は、「遊び」の仲間と「やるべきこと」の仲間から選択すると「いろいろなこと」になる。「遊び」だけ、あるいは「やるべきこと」だけから選んだりすることも間違いではないが、「遊び」と「やるべきこと」から選んだほうが、より「いろいろなこと」を説明できる。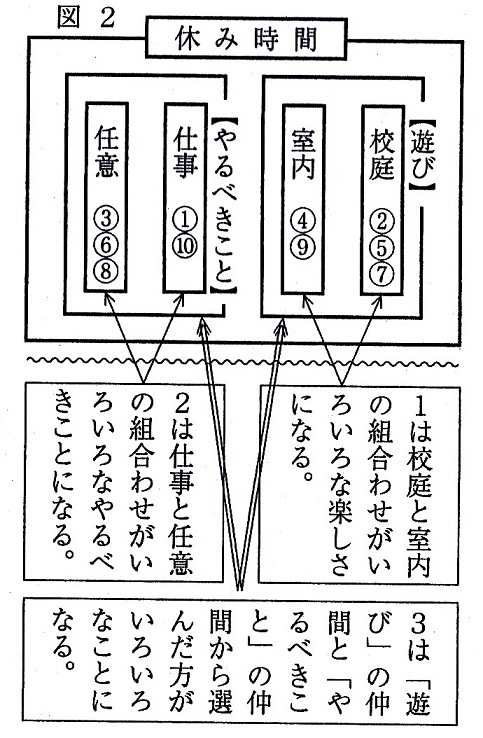
編集後記
帰納推論は、私たちが何かを説明をする時に何気なく使っている方法です。改めて言葉にされると「たしかに」と思ってしまう性質ばかりで、児童にとって「多様性」は理解しづらい、というのは私には意外でした。
「カテゴリに基づく帰納推論」とか「多様性」とかいう言葉自体を児童が理解する必要はないと思います。しかし、日常で使うレベルにおとしたときに「イメージがわく」だけで、説明文に対する理解がだいぶ違うのではないでしょうか。
(編集・文責:EDUPEDIA編集部 高橋遼)
実践者紹介
見目宗弘(けんもくむねひろ)先生
栃木県日光市立落合西小教諭。
第61回読売教育賞最優秀賞受賞。(受賞内容は「意見を持たせる国語科教育」)
この記事の出典…「説明文の「なか」の具体例をいかに選択するか—児童に帰納の知識を教え、結論の「確からしさ」を高める取り組み—」宇都宮大学国語教育学会『宇大国語論究』(23)より(2012)









コメント