中1数学「正負の数」導入・四則演算の指導案～コンセプトの統一によってつまずきをフォロー～

1　はじめに

この記事では中1数学の「正負の数」の指導案を紹介します。

2　授業のねらい

教科書のカリキュラム作成資料を改めて見てみましょう。この単元の前半は

（1）負の数の存在を知る
（2）負の数の意味を知る
（3）負の数の必要性を知る
（4）負の数を含む四則演算をできるようになる

という一続きの内容になっていることが分かります。
「負の数」は、高等学校で学ぶ「虚数」ほどではないにせよ、やはり一部の生徒にとっては修得の難しい内容です。単元の先の方まで進んだときにふと分からなくなって、少し前の内容の質問をしたくなる生徒もいるでしょう。したがって、（1）が分かったら（2）、（2）が分かったら（3）、のように区切りながら指導するのではなく、むしろ（1）～（4）をひとまとまりに捉え、行きつ戻りつできる状態を保って指導していくことが必要です。そのためには、前の段階に戻ろうと思ったときにシームレスに戻れるよう、「数を数直線上の矢印として示す」という統一的なコンセプトで指導しておくことが大切です。

3　指導のポイント・流れ

導入はセ氏温度などで

負の数の存在を示す一番分かりやすい例は、やはりセ氏温度でしょう。例えば冬が近づいてきたときを想定し「今日は最高気温が5℃でした。明日から毎日1℃ずつ下がっていくと、気温はどうなるでしょう？」といった問いかけをし、

5℃→4℃→3℃→2℃→1℃→0℃→？？？

という風に生徒に答えてもらうとよいでしょう。ここで「マイナス1℃」という表現を知らない生徒がいる可能性もあります。そういったことが予想される場合には、あらかじめ冷水に温度計を挿しておき、たくさんの氷と塩を投入して温度を0℃より下げていくというミニ実験をしてみるのも効果的です。

後に数直線が多々出てくることに備えて、わざと温度計を横向きにして温度を示す局面もあるとなお効果的です。

他にも「基準点からの高さ」を題材にするのもよいですね。教室前方にいくつかマグネットを貼っておき、「この教卓を基準にすると、このマグネットの高さはいくらかな？」などと問いかけましょう。教卓より10cm低い位置にあるマグネットを指して「10cm低いときは、高さをマイナス10cmと言うことにします」という風に導入することができるでしょう。

ここで重要なのは「確かに0より小さな何かが存在している」「それを表すためにマイナス（-）という記号を用いる」ということを知ってもらうことだけですので、あまりそれ以上に欲張った目標設定はしない方がよいでしょう。

数を「数直線上の矢印」で表す

この先が統一的なコンセプトです。本記事でおすすめするのは、数を数直線上の「点」で表すのではなく、「原点から引いた矢印」で表すことです。これは高等学校の「位置ベクトル」に相当するものですので、履修範囲から逸脱しているような気がするかもしれませんが、「ベクトル」などの難しい用語を使わなければ「そういうものか」と生徒も受け容れてくれるはずです。

導入時に温度計や高さを用いたのであれば、まさにそのままのイメージです。黒板に横向きに温度計の絵を描き、温度が0℃より高い場合は「0」から右向きに矢印を伸ばして「3℃」などと書き、0℃より低い場合は「0」から左向きに矢印を伸ばして「-2℃」などと書く、という作法を浸透させましょう。

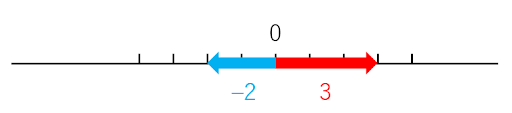
数を足すのは「矢印をそのままつなぐ」

ここまでがクリアできればこの先はスムーズに進みます。

例えば「2+3=5」のように既知の計算をまず題材にして「矢印で考えると、これって【右2の矢印】の先から【右3の矢印】をつなげて、【右5の矢印】にしていることになるね」ということからスタートしましょう。

そして「同じように考えたら、-2と-3を足すとどうなるだろうか？」と投げかけてみましょう。

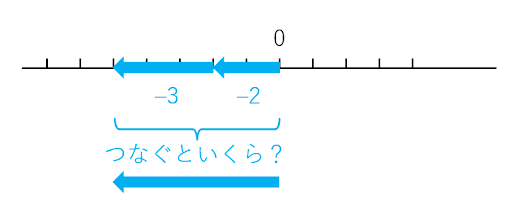
ここで注意点があります。いきなり

（-2）+（-3）=

のように数学記号を使うと記号の意味の説明が必要になってしまうので、まずは言葉でスタートします。もちろんこの場合は【左2の矢印】の先に【左3の矢印】をつなぐことになるので、自然と【左5の矢印】、すなわち-5という数が生み出されることが伝わると思います。これを数式で「（-2）+（-3）=-5」のように表すという話は、焦って出す必要はありません。1つの時限の終わりに出すぐらいでもよいでしょう。

同様にして「6に-4を足すとどうなる？」「-3に5を足すとどうなる？」「3に-5を足すとどうなる？」などと、少しずつ難しい内容にチャレンジしてもらいましょう。ときおり温度や高さなどの例に戻りながら、「今日は-3℃なんだけど、明日は今日より5℃上がるとどうなるかな？」という風に具体的事象とつなげることも有効です。ただ、いずれにしてもこの後たくさんの抽象的な計算練習を行うので、あまり具体例にこだわりすぎなくても大丈夫です。

数を引くのは「矢印をひっくり返してつなぐ」

ここも既知の計算、例えば「5-2=3」を題材として、「2を引く」という行為は【右2の矢印】をひっくり返してつなぐことと同じですね、というところからスタートするとよいでしょう。

加法の時と同様に「-2から-3を引くとどうなるだろうか？」など、少しずつ難しい例に踏み込んでいきましょう。

数式として「-2-（-3）=」と書くということや、機械的操作（例えばマイナスが2つ続いたらプラスにするなど）に習熟してもらう時間も必要ですが、機械的操作の指導を焦りすぎると「答えは出るが何をしているか分からない」という状態になってしまいますので、意味の理解と機械的操作の習熟のバランスをできるだけ取りましょう。このあたりはクラスの学力状況によってさじ加減が異なるでしょうから、本記事では深入りしません。

正の定数倍は「矢印の長さを定数倍に」

次は乗法です。基準点からの高さという事例を思い出してもらうのがよいと思います。例えば「3cmの高さ」を2倍にすると6cmであるということから、「数を2倍するということは、矢印の長さを2倍にすることと同じだな」と思ってもらえればよいでしょう。

次は「-3cmの高さ（つまり基準点より3cm低い）を2倍にするとどうなるか？」というような問いかけがよいでしょう。ほとんどの生徒は「基準点より6cm低い」という位置をイメージできると思います。それはつまり「矢印の長さを（向きはそのままで）2倍にした」のと同じことです。

負の定数倍は「矢印を反対向きにして定数倍に」

負の数をかける際のルールの説明には少し注意が必要かもしれません。例えば「3cmの高さをマイナス2倍する」というのはどういう意味なのか、この時点で「分かっている」生徒はいませんので、不用意に「どうなるかな？」と聞いてしまうと各生徒の思いを聞き出すことになってしまいます。「思い」は否定できませんので、先生が示したいのと違う「思い」が出てきたときに困ってしまうということがあり得ます。

ですから負の数をかけることを導入する際には、「こういうルールになっています」ということをはっきり宣言した上で、矢印を反対向きにして長さを調節する操作を示すのがよろしいでしょう。

4　まとめ

本記事では、中1数学で「正負の数」の導入から四則演算までをシームレスに指導するための案を示しました。「数を数直線上の矢印として示す」というスタイルで統一することにより、途中でつまずいても前の段階に容易に戻れるようになっています。参考になれば幸いです。

5　記事執筆者のプロフィール

遠藤耕一
塾講師として理系科目を20年以上にわたって指導中。生徒に学力が定着するための様々な工夫を考案し、指導に活かしている。