1 はじめに
こちらの記事は、静岡県で30年間以上続く教員サークル、シリウスのホームページに掲載されている教育実践法の一つをご紹介しています。
http://homepage1.nifty.com/moritake/
2 実践内容
分数のたし算・引き算の学習をしている。ここでは約分と通分が確実にできることがポイントになる。通分で大切なポイントは、公約数を見つけることである。そこで公約数を出したのち、枝分れを使って枝分れの計算のしかたを教えた。
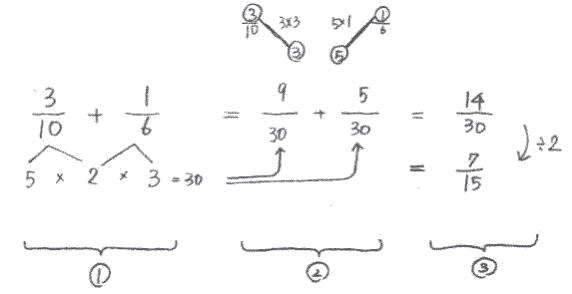
①について
・10と6の両方を割れる公約数(2)を見つけ、中央に書く。
・公約数にあといくつをかけたら、分母と同じ数になるが枝分れで書く。
・3つの数をかけると、通分する分母が見つかる。
②について
・分子と枝分れの数をたすきがけでかける。(3×3)(1×5)
・これが通分したときの分子(9,5)になる。
③について
・分子どうしをたす。(9+5=14)
・1の枝分れ(5×2×3)の中に割れる数があったら約分をする。
3 プロフィール
静岡県教育サークル シリウス
1984年創立。
「理論より実践を語る」「子どもの事実で語る」「小さな事実から大きな結論を導かない」これがサークルの主な柱です。
最近では、技術だけではない理論の大切さも感じています。それは「子どもをよくみる」という誰もがしている当たり前のことでした。思想、信条関係なし。「子どもにとってより価値ある教師になりたい」という願いだけを共有しています。
4 書籍のご紹介
「教室掲示 レイアウトアイデア事典」(明治図書2014/2/21発売)
「学級&授業ゲームアイデア事典」(2014/7/25発売)
「係活動システム&アイデア事典」(2015/2/27発売)
「学級開きルール&アイデア事典」(2015/3/12発売)
5 編集後記
計算問題でつまずいてしまったとき、なにか機械的に計算できる方法があれば身につきやすそうですよね。この実践を使えば、分数が不得意な子どもたちも苦手を克服できるのではないでしょうか。
ぜひお試しください。
(編集・文責:EDUPEDIA編集部 横山尚人)







コメント