1 はじめに
こちらの記事は、静岡県で30年間以上続く教員サークル、シリウスのホームページに掲載されている教育実践法の一つをご紹介しています。
http://homepage1.nifty.com/moritake/
2 実践内容
かけ算の意味をようかん問題で
分数のかけ算×分数のかけ算について学習をしました。この計算は、
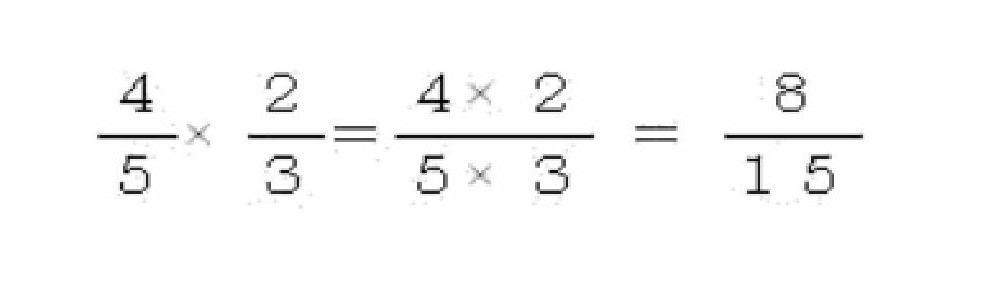
のように、分母は分母同士、分子は分子同士をかければ良い計算で、やり方は簡単です。
しかし、この式の意味を説明しようとすると、なかなか難しいです。
教科書では、塀にペンキを塗る問題を扱っていますが、授業ではようかんの問題で考えました。
戸だなに、ようかんが、1本ありました。このようかんを家族3人で食べるとき、一人分はどのくらいの分量になるでしょうか?(※青色=教師の発問/以下同様)
身近なモノを使うと、子どもたちの意欲が違います。
本物のようかんを1本出して、そのうち1/5は「これはもう誰かが食べちゃった分」と切り分けました。
残った分は4/5本。子どもたちは欲しそうに、じーっと見ています。
子どもたちは図を描いて考え始めました。多くの子が考えたのは、
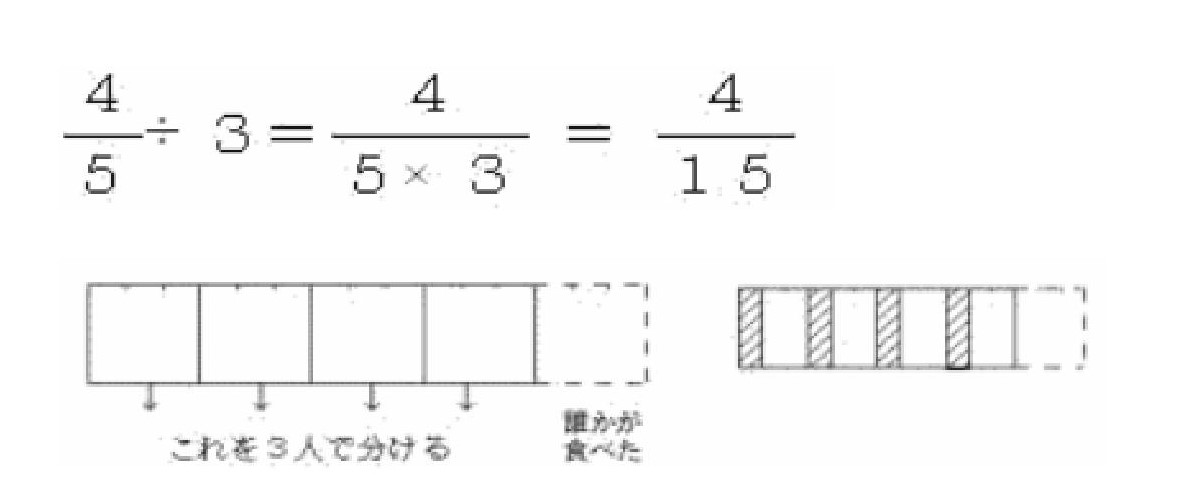
でした。
図から1/3が出てきたので、
4/5÷3の÷3は、4/5×□ と表せるでしょうか?
と尋ね、4/5÷3=4/5×1/3であることを確かめました。次に、
3人で分けたあと、一人が「いらない」と言ったので、二人分をゲットできました。ようかんを全部でどのくらい食べられるでしょうか?
今度は積み木を使って考えてみました。
4/5本のようかんを3人で分けると、一人分は4/15になりました。
それを二人分ゲットしたことを積み木を使って確かめました。
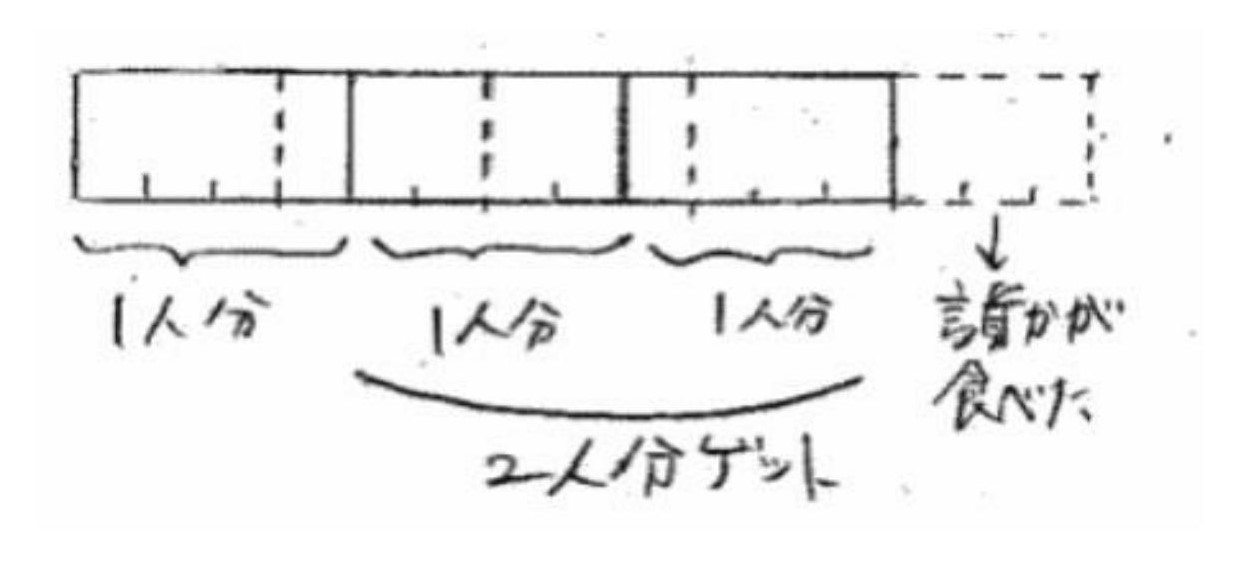
- ようかんを3等分した(÷3)そして三等分したうちの二つをもらった。つまり2つ分の人と1つ分の人が出てくる。なので、3等分したうちの2つもらったわけで、3つ分の1つが2つで2/3。それで4/5×2/3
- 12/15÷3=4/5×2つもらった/3人分=4×2/5×3=8/15 ボクがもらった分
- 4/5÷3×2=4/5×2/3=8/15
- 3等分したうちの2人分をもらったから4/5×2/3=8/15
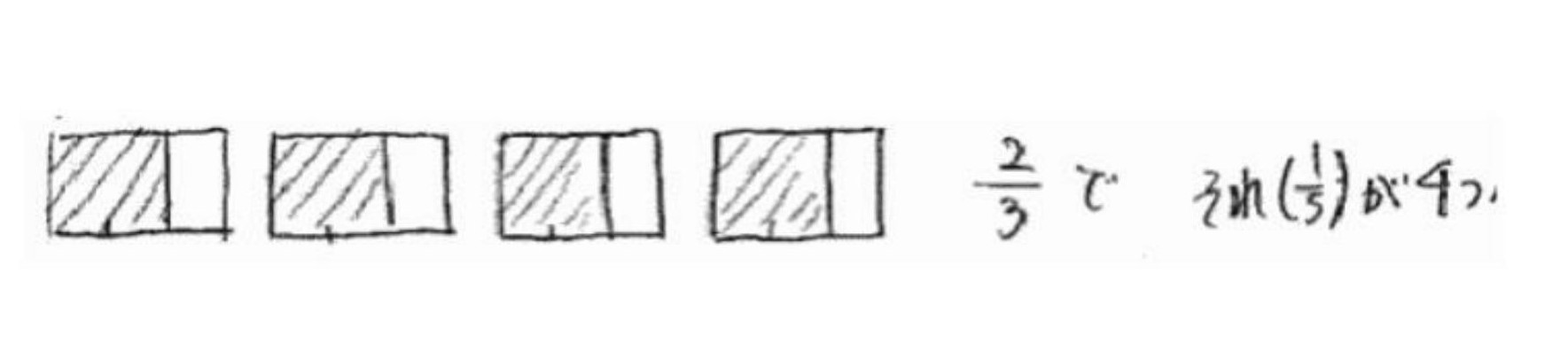
わり算の意味をクッキー問題で
分数÷分数ののわり算では、わる数をひっくり返してかけます。
どうしてそうなるのかを「クッキー問題」で考えました。
クッキーが6枚ありました。 それを一人に2枚ずつあげます。何人に分けられるでしょうか?
まずは整数÷整数を図で考えてみました。
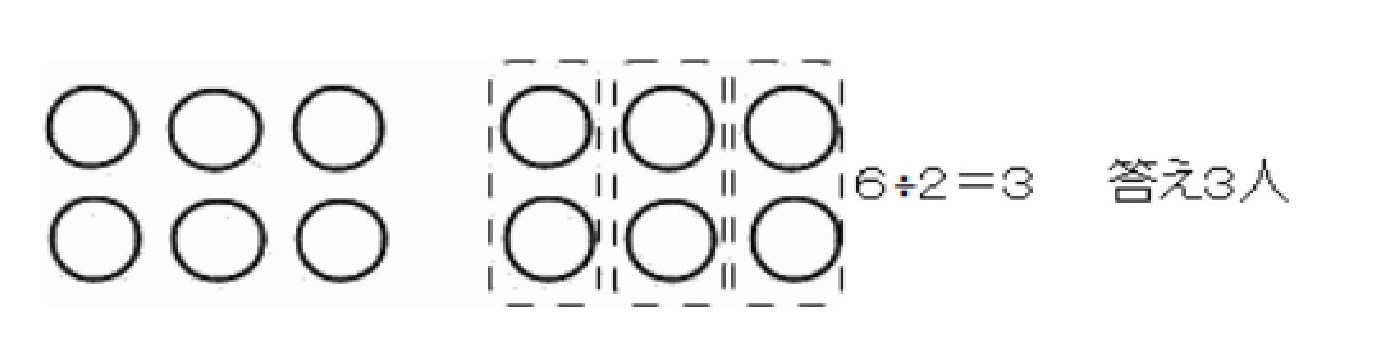
クッキーが6枚ありました。それを一人に1/2枚ずつあげます。何人に分けられるでしょうか?
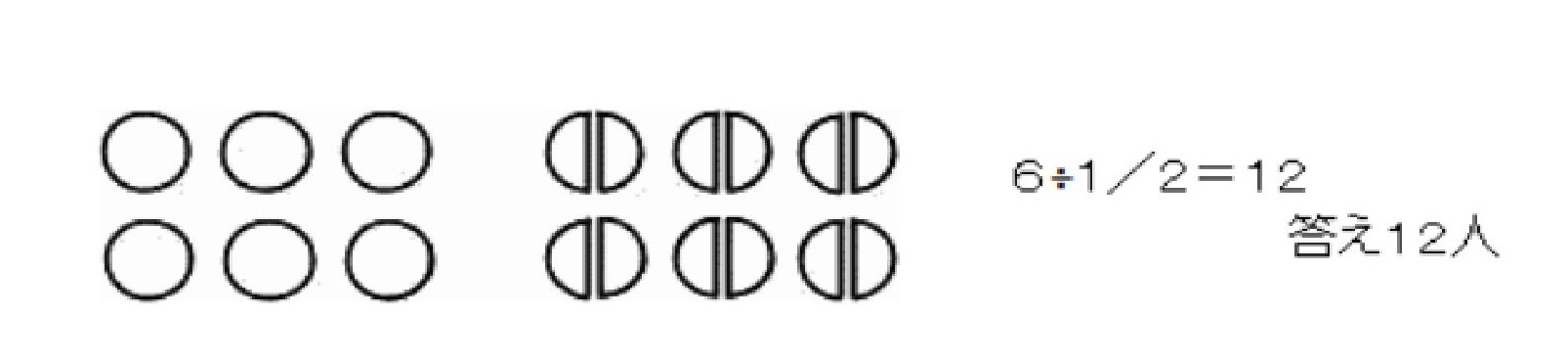
これも図を使って考えました。
1枚の半分ずつなので、12人に分けられることが分かりました。
さて次に、
クッキーが6枚ありました。それを一人に1/4枚ずつあげます。何人に分けられるでしょうか?
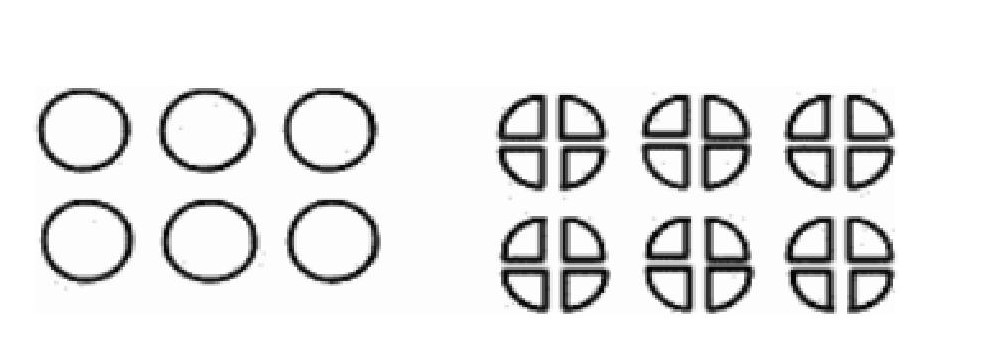
図を描いてみると、24人分になることがわかります。
6と1/4の関係に注目した子が何人かいました。
- 6÷1/4=24 答え24人
- 4(1枚で4人に)×6(枚ある)=24
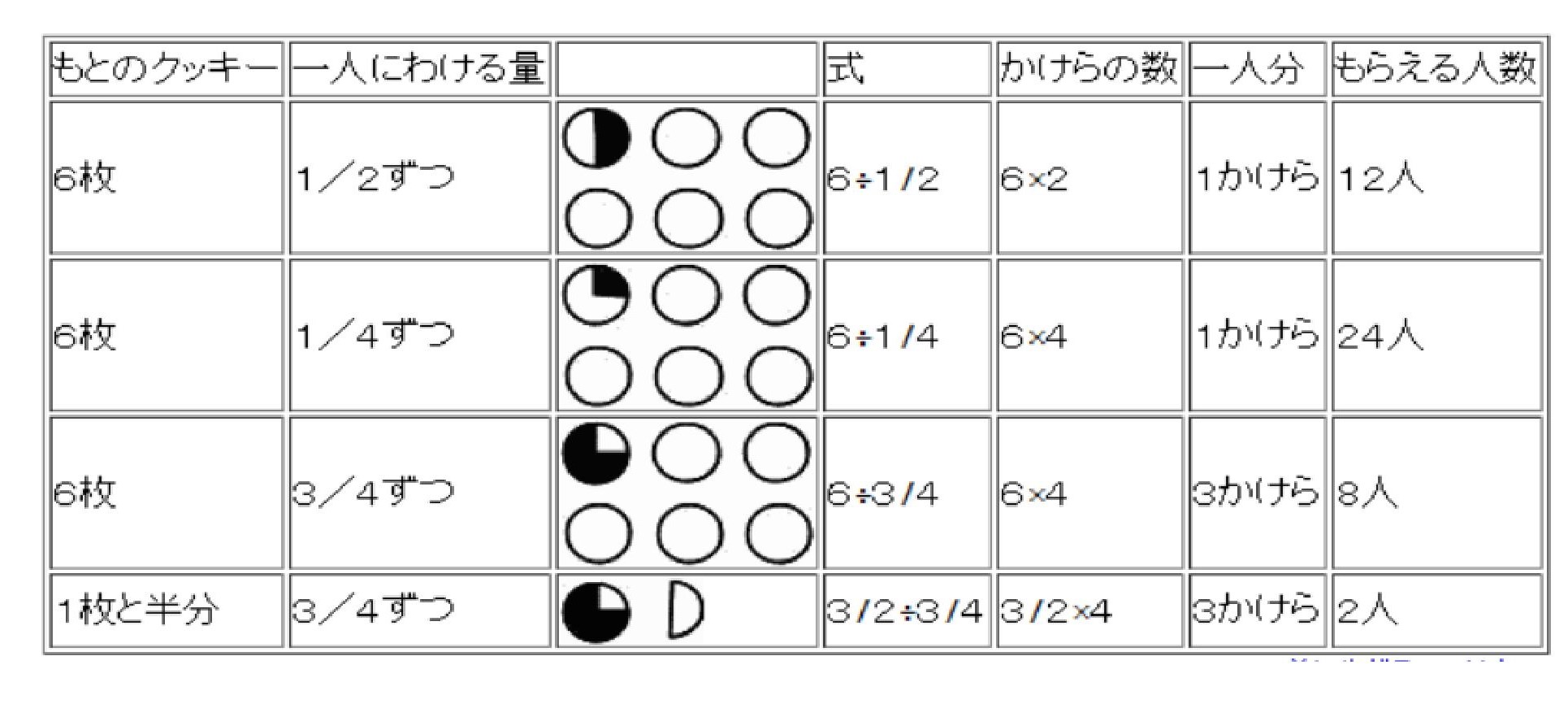
クッキーが6枚ありました。それを一人に3/4枚ずつあげます。何人に分けられるでしょうか?
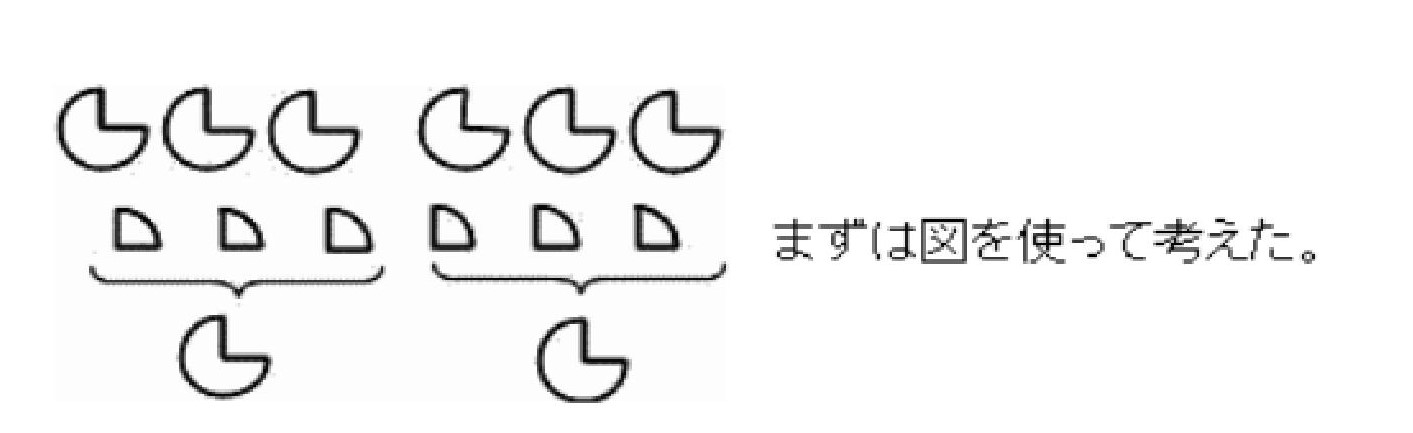
2人の考えのように、1枚のクッキーを4つにわけて、そこから3つ分ずつ取り分けていくと、8人に配ることができます。
また6と3/4の関係に注目した子もいました。
- 3/4÷6=3/24=1/8でもこれだと1/8人になってしまっておかしいから、ひっくり返して8人にした。
- まず最初のクッキーを1/4にする。1/4のクッキーは1枚で4つだから、4×6,次に4×6=24に分けたクッキーから一人分の3つずつを分けるから、24÷3=8だから8人分に分けられる。
二人の話に「ひっくり返す」「かける」という話が出てきました。
これを、6÷3/4=6×4(24に分ける)/3(3つずつ配る)=8
になると気づき、どうも「ひっくり返してかけるらしい」ということになりました。
そこで今度は、
クッキーが6枚ありました。それを一人に3/8枚ずつあげます。何人に分けられるでしょうか?
ひっくり返してかけてみると、図を使って確かめてみると、確かに16人に分けられることが分かりました。
式の意味を分かりやすくするために
分数÷分数は「ひっくり返してかける」。
でも改めて「どうして?」と問われると、なかなか答えづらいです。
少しでも「ひっくり返してかける」の意味がイメージできるように、もう少しクッキー問題で考えました。
クッキーが1枚と半分ある。それを一人に3/4枚ずつわけると、何人に分けられるでしょうか?
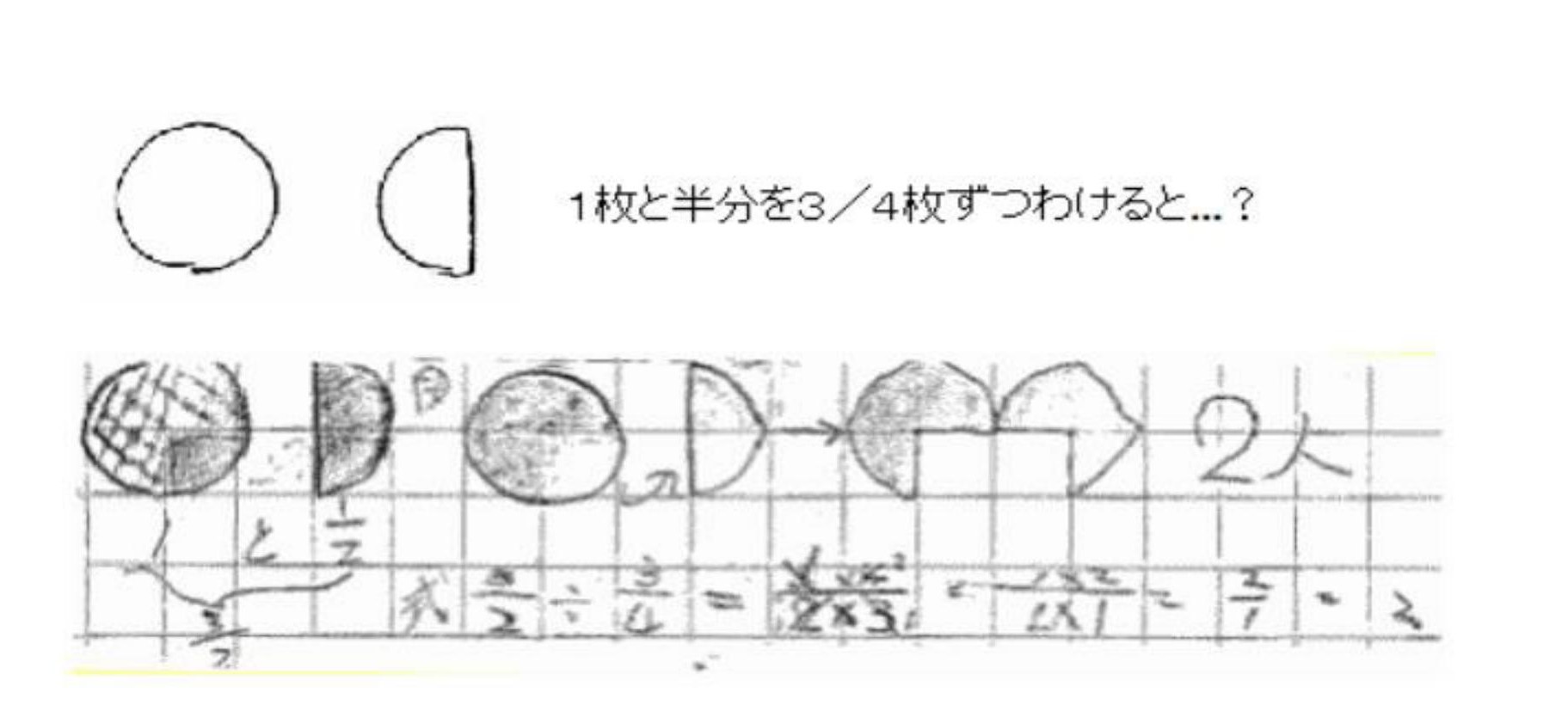
図を使って考えた子が多くいました。
図のようにクッキーを1/4かけらにして、3枚ずつ配りました。
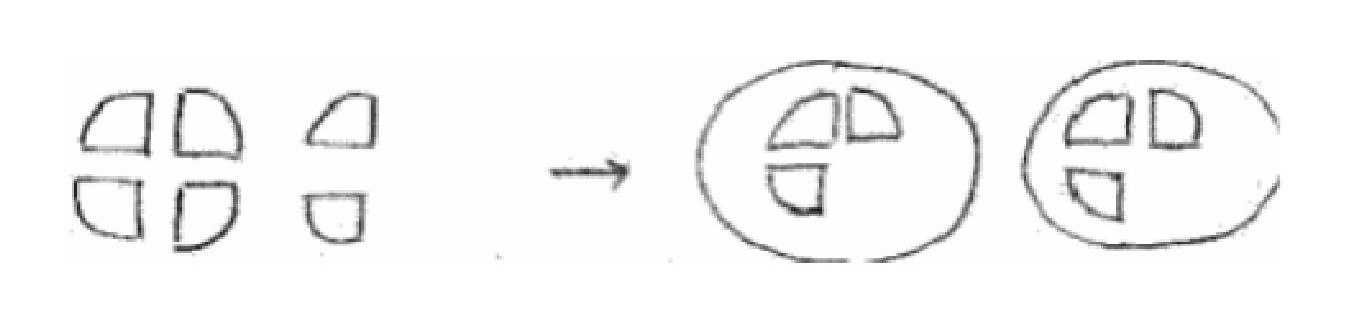
6かけらを3つずつまとめます。
これを式で考えた子がいました。
前回の「6枚を3/4ずつ分ける」のときも、ひっくり返してかけたことを生かして、
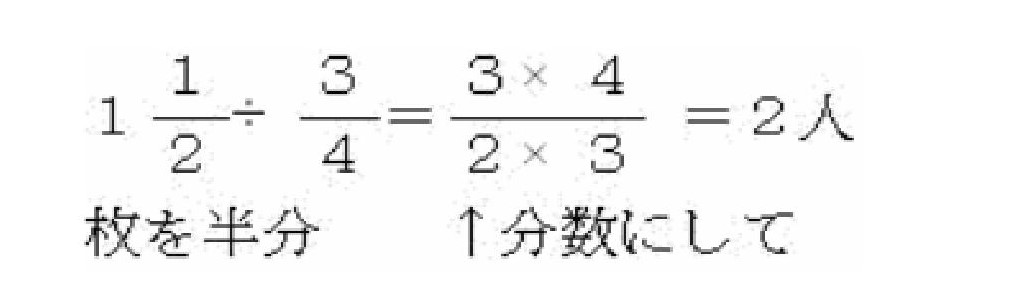
- 1枚と半分は1.5だから、1.5÷3/4=1.5÷0.75=2
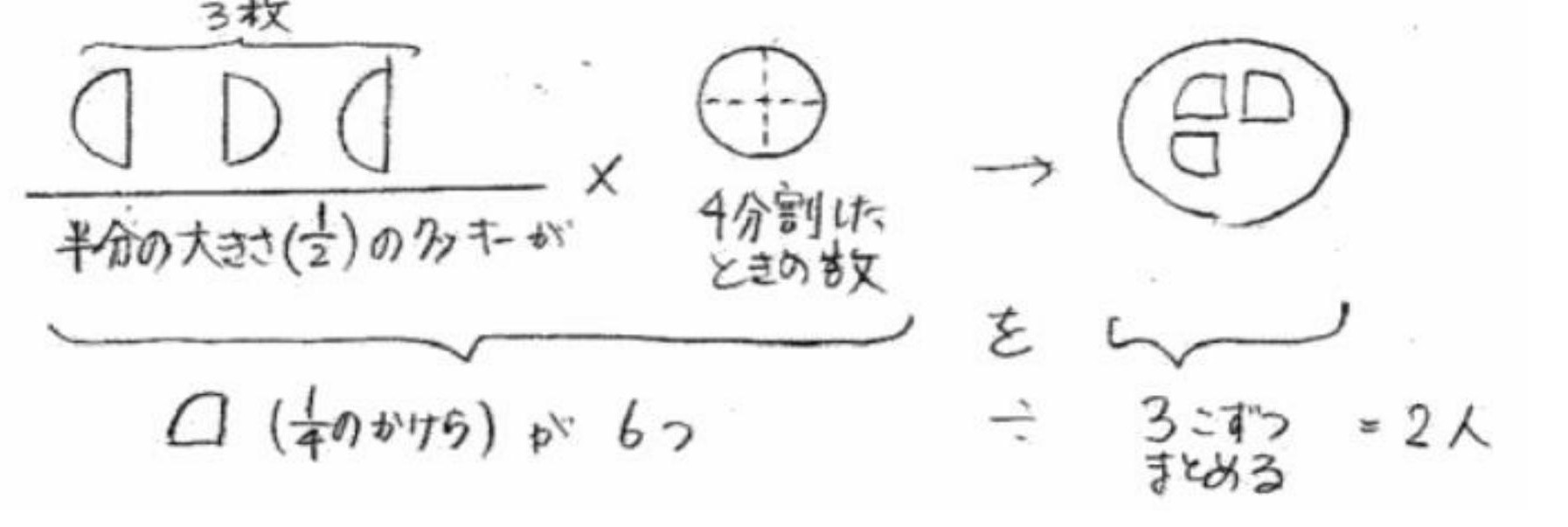
ここでもう少し、3/2×4/3=2の意味について考えてみました。
やはり前回の「6枚を3/4ずつ分ける」と同じように、
4分の1かけらを作って、3つずつにまとめていきました。
分数÷分数の計算のイメージは、
小さなかけらを作って、袋に入れてまとめていく。
とすると、図と式が結びつきやすいです。
チャンピオンを決めよう
分数のかけ算のまとめとして、ゲーム的要素を入れた計算の授業を行いました。
この単元では、分数を使ったかけ算やわり算は初めて習います。
そこで計算技能の向上を図りました。
まず最初に取り組んだのが、分数×整数です。
分数×整数の積を最大にしよう
ルール1 サイコロを振り、出た数を(1)(2)(3)の順に当てはめます。
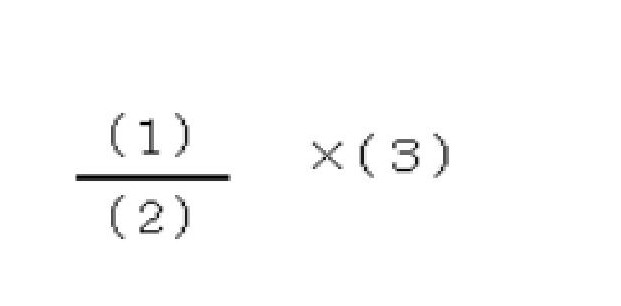
隣の人とやって出た答えの大きい方を勝ちとしました。
子どもたちは帯分数に直して比べたり、分母の大きさで比べていました。数回やったところで、
「積が15より大きくなった人はいますか?」と尋ねると、数人の子が手を挙げました。
どんなときが15以上になるのか。黒板に書いてもらうと、
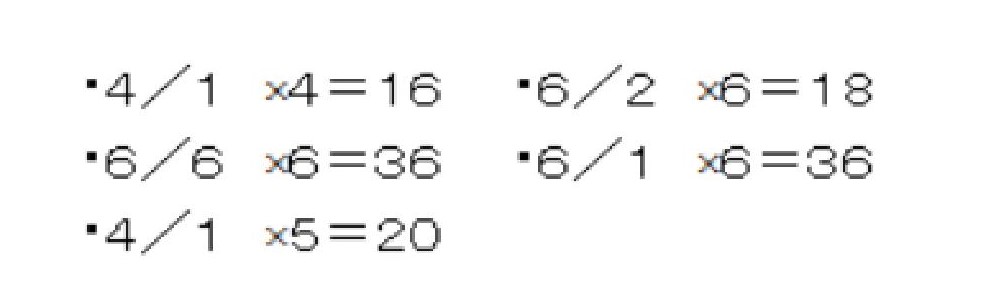
どんな数が出たときに積は大きくなりますか?と尋ねると、
- (1)が大きいとき
- (2)が小さいとき
- (1)と(3)は入れ替わっても同じ
というかけ算の性質に気がつくことができました。そこで今度は、
ルール2 サイコロも3回振った後、積が大きくなるように、場所を選んで数を当てはめる。
このように、少しルールを変えると積が大きくなるように工夫して、数を当てはめていきました。
隣の人と数回やったところで、ずっと勝ち続けている(負け続けている)人を集めて、チャンピオンを決めました。
チャンピオン大会は大いに盛り上がりました。
さて、次はわり算です。かけ算と同様に、
分数÷整数の商を最小にしよう。
ルール1 サイコロを振り、出た数を(1)(2)(3)の順に当てはめる。
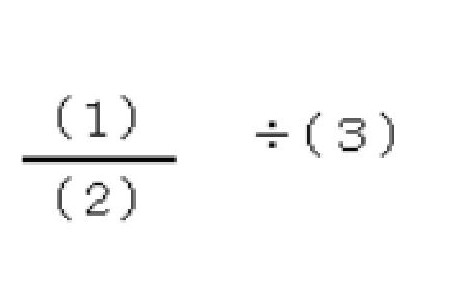
サイコロを3回振った後、商が小さくなるように数を当てはめます。
まずは上のやり方で数回やった後に、
2/4 ÷6=1/12 のように商が1/12より小さなった人はいますか。どんな数が出たときに商は小さくなりますか?と尋ね、
商が小さくなる場合について考えました。
積の場合とは逆に、
- (1)が小さいとき
- (2)が大きいとき
- (2)と(3)は、入れ替えても同じ。
であると良いことに気づきました。
このことを確認した後、より小さな商を作りました。
最後に取り組んだのは、帯分数の計算です。
帯分数×整数の積を最大にしよう。
しかし、帯分数のかけ算についてはまだ習っていないので、どう計算したら良いのか正しい答えが出るかについて学ぶことができました。
授業の感想を書こう。
- 私はこれをやったとき楽しいと思って、どうやったら大きくなるかとか、小さくなるかとかいろいろ考えながらやりました。かけ算の場合は、分母を小さくして分子が大きいと最大の数が出ました。
- 自分で考えて数字を入れ替えるとき、本当にこれで最大なのか最小なのかを考えながら入れていきました。この授業は楽しくやりながらも、計算しながらやっていくのでとてもいいと思ったし、とても楽しかったです。
- ぼくは最初は、どの数字がどこに入っても答えは同じだろうと思っていました。でも実際にやってみると、全然答えが違っていてびっくりしました。いろいろな数の組み合わせができて楽しかったです。
- 最後にやった帯分数のでは、72までいくのですごいと思いました。あと全部数字が大きくでもだめだと思いました。
- 今日までやってきた算数の中で、一番楽しかった算数だと思います。また機会があればやりたいです。
3 プロフィール
静岡県教育サークル シリウス
1984年創立。
「理論より実践を語る」「子どもの事実で語る」「小さな事実から大きな結論を導かない」これがサークルの主な柱です。
最近では、技術だけではない理論の大切さも感じています。それは「子どもをよくみる」という誰もがしている当たり前のことでした。思想、信条関係なし。「子どもにとってより価値ある教師になりたい」という願いだけを共有しています。
4 書籍のご紹介
「教室掲示 レイアウトアイデア事典」(明治図書2014/2/21発売)
「学級&授業ゲームアイデア事典」(2014/7/25発売)
「係活動システム&アイデア事典」(2015/2/27発売)
「学級開きルール&アイデア事典」(2015/3/12発売)
5 編集後記
分数というと、ここでつまづく子どもが多いのではないでしょうか?
それを食べ物という身近なものを分けることで、分数の仕組みから理解させています。
また皆で楽しめるゲームを取り入れることで、分数の知識が定着したのではないでしょうか。
(編集・文責:EDUPEDIA編集部 河村寛希)







コメント