1 概要
この実践は(株)教育同人社の許可を得て、「はなまるサポート」の学習指導ポイント一覧より転載しています。
実践の続き(無料)は記事末尾のURL からご覧ください。
また、以下より実践をPDFでダウンロードできます。
添付ファイル
2 指導の前に
(1) 数えることの意味
まず、「数えることができる」とはどのようなことなのでしょうか。普段何気なく数えていることをきちんと整理しておきましょう。
① 数詞が唱えられる。
② 数詞と数える対象とを、1対1対応ができる。
③ ②で対応させた最後の数詞が対応したものの全体の個数を表すことを知る。
④ ②で対応させた数詞がそのものの順序を表すことを知る。
⑤ 他のものを加えたり一部を取り除いたりしなければ、数えたものを並べ替えたりまとめたりしても個数は変わらないことを認める。
⑥ 数える対象の集合を明確にとらえる。
(2) 数え方の工夫
ただ単に「数える」と言ってもそこには工夫が発生します。その工夫を突き動かす原動力は「思考の節約、労力の節約」でしょう。そのための工夫をまとめます。
① 適当な観点によって分類して数える。
② 適当な大きさにまとめて数える。
③ 数えるものと関数関係(1対1対応)にある数えやすいものに置き換えて数える。
(3) 「数」の表し方
工夫して数えた数値をどのようにして伝えたらよいのでしょうか。書いて伝える方法と、読んで伝える方法があります。この単元では、位取り表の指導をします。そこで明確にしたいことは、十進記数法と位取り記数法のミックスが十進位取り記数法だということです。
そのために、十進記数法の経験をした後に十進位取り記数法を指導する流れを考えました。
① 十進記数法
ある数の個数が10まとまったとき、別の単位を作る数の表し方、つまり10個のまとまりのまとまりを作る考え方です。
例えばエジプトの記数法は下図のようになっています。
また、「一円」「十円」「百円」「千円」「一万円」などのお金も十進記数法で表されていると考えられます。これらは、「10のまとまり」のまとまりで名称や記号が作られ、それを用いて表すのですから、記号の「種類」が問題で、「書く位置」は関係ありません。また、タイルなどで、1個、1本、1枚、1束という風に決める考え方も十進記数法の1つと言えます。
漢数字も十進記数法と1つと言えなくもないのですが、下の表からも分かるように、これは「十進法」と「万進法」の組み合わせによる表記法なのです。ちなみに我が国ではこの漢数字による表記法をもとにして命数法(数の読み方)を規定しています。
② 位取り記数法
数字を書く位置によってその単位が決まる記数法です。つまり、単位を表す新しい記号は必要としないのです。必要なことは数字を書く場所をはっきりと決めることなのです。
例えば、数量が3056個あった場合、それを位取り記数法によって表す場合、1~9個までの部屋、10個~90個までの部屋…という風に左に部屋を1つずつ決めていきます。10個で1つ上の単位になる場合は、左の部屋に1つ繰り上がる約束です。つまり、各部屋にはその単位の個数を記入すればよいのであり、その個数が無いところ(「空位」)には、空位を表す「0」を書くのです。そして、全体の
数量は、
10×3+1032×0+101×5+100×6 で表されます。
上の位取り記数法は、10個になったら左の位に1つ進むので、十進位取り記数法と呼ばれています。
3 指導の実際
それでは指導計画に従って指導を展開しましょう。本時は、次の目標の下に展開します。
- 十進記数法を経験させる。
- 十進位取り記数法の良さを理解させる。
(1) 問題提示
「先生のおともだちからみかんが1はことどきました。これだけでした。」
(と言って模造紙にかいた絵を広げる。)
「去年も頂いたのですが、何個だったかわすれてしまいました。今年はぜったい忘れないようにノートに書いておきたいと思います。」
「まず何個あるのか、みんなで上手に数えてくださいませんか。」
(と言って26個のみかんがかいてあるプリントを配る。)
(2) 自力解決①
T1 「いくつになりましたか。」
「どのようにして数えましたか。」
C1 10のまとまりを囲んで数える。「にじゅうろく」です。
C2 みかんに,1、2、3 …と書き込んで10までが2つとあと6だから「にじゅうろく」です。
C3 「いち、に、さん、し…」と数詞を唱えていって「にじゅうろく」です。
T2 (総数を確認して)「今年は絶対忘れないようにノートに書いておきたいと思います。
どんなふうにしたらよいでしょう。」
C4 「にじゅうろくと書く」「絵を書いておく」「○で書く」「数字で書く」など。
T2 「じつは、昨日、先生は夜、魔法使いの夢をみたのです。その夢で魔法使いはこんなことを言いました。
『ねえねえ、先生、ここに8個のおはじきがあるんだけどさ。これで「にじゅうろく」を表せないかな。おはじきにチョイとまほうをかければ、この8個のおはじきで「にじゅうろく」がわかるようにできるんだけど。明日子どもたちにきいてごらん。きっと分かるよ。』
というものでした。ここに、おはじきを8個用意しました。さて、みなさん、これで「にじゅうろく」が表せますか?」
(3) 課題の意識化
めあて・・・「にじゅうろく」のあらわしかたをかんがえる。
T3 きょうは、「にじゅうろく」のあらわしかたをかんがえましょう。
まず、この「へんしんおはじき」を8こつかってあらわしてみましょう。
何個をどのように変身させたら「にじゅうろく」になるか、工夫してノートに書いてみましょう。
(4) 自力解決②
※留意点
個別に観察をします。やり方があまり分からないようだったら、たとえば「大きさ変身」でのアイディアを、途中で示します。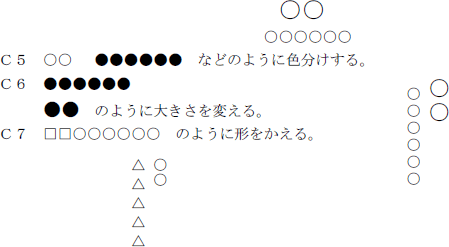
(5) 学び合い(発表・検討)
自立解決の結果を発表させます。
- 形や大きさ、色を変えたりして「10のまとまり」と「ばら」の区別をしていることを評価します。
- そしてこのやり方では、位置が関係ないことを強調します。どう置いても26こに変わりはないことを確認します。
T5 「なるほど、このような工夫だったらノートに書いておけますね。みなさんとてもよく考えてくれました。やっぱり魔法使いが言っていたことは正しかったんですね。」
T6 「ところで、今までは「へんしんおはじき」をつかいました。ところがおはじきの魔法が解けて、変身しなくなってしまいました。さて、こまった。もっと違う工夫はないでしょうか。」
と言って、全く同じおはじきを8こで工夫できないか考えさせます。そして、「位置」の指導をします。
このように、書く場所をきめておけば、おはじきが変身しなくてもよいことを説明します。
その後、部屋の名前を「十の位」「一の位」ということを指導します。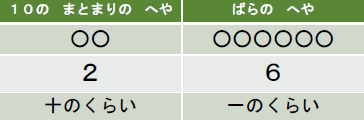
(6) まとめ
T7 「今日の勉強では、「にじゅうろく」の表し方にもいろいろなやり方があることが分かりました。どんな表し方でしたか?」
C9 形や大きさを変えると26個は、8個で表せます。
C10 形を変えないで、おはじきをおく場所を決めてもいいです。
C11 位取り表を使います。
C12 数字で26と書きます。
C13 「2」は十の位、「6」は一の位を表す数です。
※置き換えるのは「十進記数法」のよさで、位置で決めるのが「位取り記数法」のよさであることを強調します。
参考文献
算数教育の新しい体系と課題(シリーズ、全10巻)
2 数学的な考え方を育てる「数」の指導 片桐重男著 明治図書(1995年)
4 実践者紹介
山﨑 憲
元東京都算数教育研究会会長。
「小学校時代から現在までで,今が最も算数がすき」と,小学校退職後も算数教育に没頭し,現職時代に引き続き年に数回研究授業も試みている。
現在東京学芸大学講師として初等算数科教育法を担当。
またボランティアとして東村山市算数教室を開催し算数好きの子どもの育成を目指している。
5 サービス紹介
同社の「はなまるサポート」では、若い先生のための授業ヒント集として、毎月の学習指導ポイントを細かく解説しています。また、不明点や疑問点などを無料で相談を受け付けています。
(編集・文責:EDUPEDIA編集部 佐藤 睦)









コメント