1 はじめに
こちらの記事は、静岡県で30年間以上続く教員サークル、シリウスのホームページに掲載されている教育実践法の一つをご紹介しています。
http://homepage1.nifty.com/moritake/
2 二桁のかけ算 ~不思議なかけ算~
二桁のかけ算の発展的な学習として不思議なかけ算に挑戦した。まず、最初の問題は十の位と一の位を入れ替えた数字の積は等しくなる、という問題である。
発問1:36×42と63×24の答えは同じになると思いますか。
一人を除いた全員が〈違う〉と予想した。これまでの経験でそう感じている。
そこで実際に計算してみると、
36×42=1512
63×24=1512
どちらも同じ答えになった。「えー!、同じ答えになったよ」という声が起きた。そこで、
発問2:ほかにもひっくり返して、同じ答えになる計算があるか探してみよう。
いきなりこうした数の組み合わせを見つけるのは難しいので、電卓を使うことにした。少しずつヒントを出していて、その答えが、
34×86=2924
43×68=2924
であることを突き止めた。でも、どうしてこんなことになるのだろう。筆算を図のように、詳しく書くと、どちらも24,18,32,24が出てくる。
正確には、24,180,320,2400で、18,32が180,320のように同じ桁のところで交換しているだけなので、答えが等しくなる。
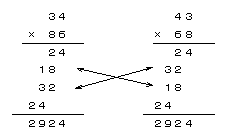
次に式の差と積の差について計算をした。
発問3:38×42と40×40の答えを比べてみよう。何か気がつくことはありますか。
40を中心とした42と38の差は、48−38=4である。答えの差は、
38×42=1596
40×40=1600 なので、
1600−1596=4 となる。
つまり式の差(42−38)と、答えの差(1600−1596)がどちらも4になっている。どちらも4だけ違うことに子どもたちはすぐに気がついた。そこで、
発問4:式で違う分だけ答えも違うのか計算してみよう。
計算練習もかね、いろいろなケースについて計算で確かめてみた。
41×39 と 40×40 1599と1600(1違い)
57×63 と 60×60 3591と3600(9違い)
このように、必ずしも式の違いが答えの違いになっていないことが分かった。
数学的には、(x−a)(x+a)=x^2−a^2 の計算をやっていることになる。試行錯誤で計算をして分類をしていけば、
ある数(40)を中心として、
1だけ違う(39と41)のときの答えの差は1(1×1)
2 (38と42) 4(2×2)
3 (37と43) 9(3×3)
4 (36と44) 16(4×4)
という決まりに気がついたかもしれない。式の差が4のときは、18×22,28×32,38×42,48×52… どれも答えの差が4になる。これも(x−a)(x+a)=x^2−a^2を計算しているからである。
最後は、少し難しい挑戦問題に取り組んだ。
発問5:□□×□□=5963になる式を見つけよう。ただし□の中は、12×34のように連続しています。
こんな問題も子どもの挑戦意欲をかき立てる。電卓片手にパチパチやっていた。手計算でやらせても良かった。あれこれ試行錯誤して、6,7,8,9であることを突き止めた。「ふー、やっと見つかった」の声も起きた。答えも「5953(ごくろうさん)と言っているよ」と声をかけると、「なんだぁ」と一同脱力した。
3 プロフィール
静岡県教育サークル シリウス
1984年創立。
「理論より実践を語る」「子どもの事実で語る」「小さな事実から大きな結論を導かない」これがサークルの主な柱です。
最近では、技術だけではない理論の大切さも感じています。それは「子どもをよくみる」という誰もがしている当たり前のことでした。思想、信条関係なし。「子どもにとってより価値ある教師になりたい」という願いだけを共有しています。
4 書籍のご紹介
「教室掲示 レイアウトアイデア事典」(明治図書2014/2/21発売)
「学級&授業ゲームアイデア事典」(2014/7/25発売)
「係活動システム&アイデア事典」(2015/2/27発売)
「学級開きルール&アイデア事典」(2015/3/12発売)
5 編集後記
算数のかけ算の実践です。一見、答えが全然違うように思えても、実は同じ答えになる数式を使って、計算の工夫の仕方を学びます。計算に苦手意識を抱いている子でも、このような数式の「不思議さ」に触れることで、ワクワクしながら学習をすることができるのではないでしょうか。本実践をぜひご活用ください。
(編集・文責:EDUPEDIA編集部 佐藤光紘)









コメント