本単元で身に付けたい資質・能力
本単元では10進位取り記数法を基に整数や小数の仕組みを考えることができる能力を養う。また、整数と小数の関係を理解する過程を振り返り、学習したことを今後の生活や学習に活用しようとする態度を育む。
単元の評価基準
- 知識・技能:0.1より小さい位の小数の表し方や仕組みを理解することができる。
- 思考・判断・表現:0.1より小さい位を含む小数の、大小関係や構成について考え、説明することができる。
- 主体的に取り組む態度:整数と小数の関係に着目し、10進位取り記数法のよさに気付き、学習したことを今後の生活や学習に活用しようとする。
まずは直感! ゲーム①「小数バトル! ピッタリ数直線」で学ぶ小数の大きさ

小数の導入では、まず「小数も一の位や十の位と同じように『分けることができる量』である」と実感させることが大切だ。
そのうえで、小数の大まかな大小関係や位置関係を直感的に捉えられるようにする。
この目標を達成するために最適なのが、ゲーム形式で楽しく学べる「小数バトル! ピッタリ数直線」。
「小数バトル! ピッタリ数直線」のルールは以下の通り。
- 各グループに0〜3までの数直線がかかれた2種類の紙を配布する。
①1目盛=0.1、②1目盛=0.01 - 数直線①のみ机上に出し、数直線②はしまわせる。
- 教員は小数(2.56等、小数第2位までの数)を板書する等して、児童に示す。
- 各児童はその小数が数直線①上のどの位置にあるかを推測し、紙にマークする。
- 全員がマークし終えたのち、数直線②で答え合わせをし、最も近い人が勝ち。
このゲームで児童は、以下の2点を自然と意識することができる。
- 2.56は2.5より大きいのか小さいのか
- 2.56は2.5と2.6の間のどのあたりに位置するのか。
前者でつまずく児童が多いと想定される場合には、数直線②を配布せず、2.5と2.6の間にある人は全員正解としても良いだろう。
その場合には教員が、「2.5と2.6の真ん中かな?」「2.56は、真ん中より少し大きいね」などとつぶやくことで、思考の言語化を促すと少しずつ児童の学びが深まる。
児童の理解度に合わせて難易度を変えられるのが、このゲームの魅力の1つだ。
数の構造にせまる! ゲーム②「何は何が何個分」で学ぶ10進位取り記数法
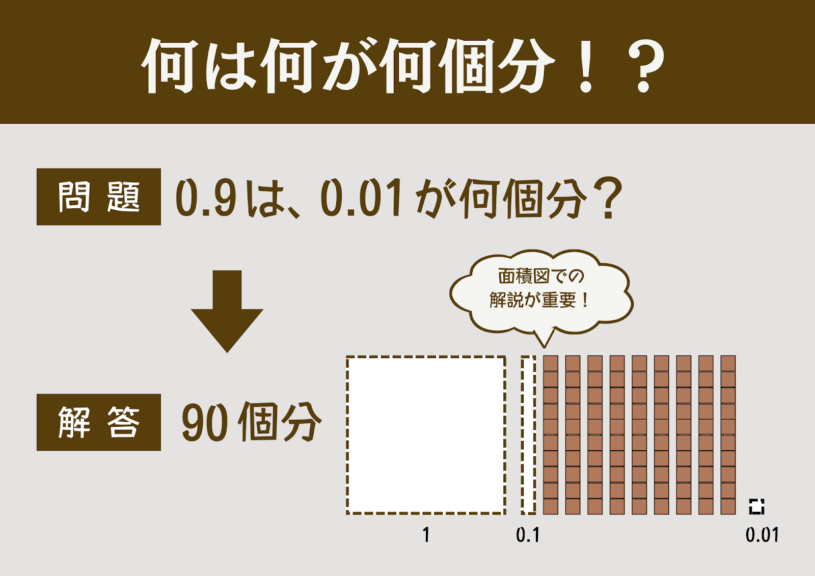
小数の「構成」を理解するゲーム「何は何が何個分」について
数直線で大まかな大小関係や位置関係の感覚をつかんだら、今度は「構成」を学ぶゲームへ。
「何は何が何個分」の形式で問題カードを出し、児童に推論させる。
例題:
- 「0.9は0.01が●個分」 → 答え:90個分
- 「●は0.01が53個分」 → 答え:0.53
カード形式にすることで、クイズ感覚で楽しめる。
また、視覚的理解を助けるために「面積図」を活用すると良い。
始めの方は、「900は10が●個分」→ 90個分という整数での例と対応させることで、ゲームの理解を深めるだけでなく、小数と整数の構造の共通性を体感できる。
小数の仕組みは「0.1のかたまりが何個か」「0.01がいくつ集まっているか」という視点から導くと、抽象的な理解につながる。
応用問題で思考力を伸ばす
基本問題に慣れてきたら、応用問題を出題しても良い。
例題:
- 「0.9は●を10個分」 → 答え:0.09
- 「0.08は0.02が●個分」 →答え:4個分
逆算の考え方や倍数の考え方が必要になるので、「これができたら+2点!」等と言って出題するのも良いだろう。
互いに問題を作りあったり、説明ができたら加点してあげたりと、児童の表現力、論理的思考力を刺激できるのがこのゲームの魅力の1つだ。
クラス内で理解度の差がある等して全体で応用問題が扱えない場合には、タブレット上で問題カードや解説カードを配布し、ペア同士で進めることもできる。
算数が苦手な児童には、面積図を用いた色塗りから始めると良い。理解の段階に応じて活動を設計し、個別最適な学びの一歩手前の課題を提示することが大切だ。
2つのゲームで得られる学びと次時への接続
この導入で児童が得られる学びは、「小数の大小関係や位置関係の感覚」と「小数の構成」だ。
| 活動 | 得られる力 |
| 小数バトル | 小数の大小関係・位置関係な量の捉え方 |
| 何は何が何個分 | 小数の構成(10進位取り記数法)への理解 |
この2つの活動により、「小数の意味」が感覚的・構造的に理解できる土台が築かれる。
次時以降の「小数のたし算・ひき算」にスムーズにつなげるためにも、有効な導入として機能する。
執筆者
まき先生
中学高校で数学を教えている。体系的に教えるためには算数から学びなおす必要があると感じ、算数の授業案についても学習をすすめている。
実践的かつつながりを意識した授業案の作成に努める。









コメント