1 概要
算数の教材を作成する際に、児童が学習内容をより理解しやすくなるように、問題の構成要素や出題の順番について心がけていることをいくつか紹介します。
<目次>
(1)「同じ条件」と「異なる数値」を使った問題
(2)美しいスモールステップ
(3)ポイント意識
2 「同じ条件」と「異なる数値」を使った問題
私も含め先生は、普段から、テストや宿題、授業教材等で、問題を作る機会が多いと思います。
その時に、「どのような問題の作り方をすれば、一番学力が付きやすくなるのか」ということについて、日頃から考えていることかと思います。
そこで、市販の教材を見てみますと、1問目から2問目になると難易度が急に上がり、3問目でまた下がっている、というように、問題の順番がややいびつになっている場合が多々あります。
私は問題を作成する際に、「きれいなステップを上手に踏ませたい」と考えています。
どのようにそのステップを踏ませていくか、以下例題を使って見ていきます。
例題(上):スーパーで、同じ値段のプリンを5個買い、次に120円のジュースを買うと、全部で520円になりました。プリン一個の値段は何円ですか。
→520円からジュースの120円を引いて、残りを5で割れば、答えは80(円)とわかります。
次に、以下の問題を解くとします。
例題(下):Aさんのクラスでは、折り紙を28人に同じ数ずつ配りました。その後、Aさんは友達から3枚もらったので、Aさんの折り紙の枚数は8枚になりました。クラス全体で、何枚の折り紙を配りましたか。
→8−3=5で、最初の一人当たりの枚数が5枚とわかります。それに、人数である28をかければ、答えは140(枚)とわかります。
よく見てみると、上の問題は、先に引き算をしてから割り算をしています。下の問題では、先に引き算をしてから掛け算をしました。条件にズレが出てきていることがわかります。
いきなり例題(上)から例題(下)へ飛んでしまうと、ややハードルが上がってしまうため、その間に以下のような問題を入れます。
例題(中):スーパーで、同じ値段のプリンを7個買い、次に100円のジュースを買うと、全部で940円になりました。プリン1個の値段はいくらですか。
条件は全く変えずに、数値だけ変えてあげることで、繰り返し同じ考え方をつかうことになります。その過程で自信をつけて、次にちゃんとステップすることが出来るのではないでしょうか。
3 美しいスモールステップ
軽→重
(1)で、「13+25」という問題を提示することとします。
この問題の次に、(6)「67+88+79」という問題を提示すると、いきなりハードルが上がってしまいます。
そのため、この2問の間に、以下の様なステップを踏んでいきます。
(2)28+53
(3)49+87
(4)21+35+10
(5)51+13+59
この問題の配置にも、ポイントがあります。
(1)は繰り上がりがありません。(2)では繰り上がりを1回、(3)では2回行います。(4)では、答えが3項になり、繰り上がりはありません。(5)では同じく答えが3項で、繰り上がりが一度起こります。(6)では、2度おこります。
易→難
比を約する問題です。
(1)「12:6」という問題の直後に(7)3/4:5/6 という問題を提示すると、いきなりハードルがあがってしまうことになります。
そこで、その2問の間に以下のような問題を入れることとします。
(2)15:27
(3)14:35:49
(4)0.8:5
(5)0.6:0.42
(6)5/8:2
(1)は、片方の数である6で割ってあげれば2:1という答えが出ます。(2)は、最大公約数の3で割ってやれば良いです。(3)は3つの数の比です。(4)は少数:整数、(5)は少数:少数、(6)は分数:整数、(7)分数:分数というように、少しずつステップがあがっています。
このように、上手にステップを踏ませていくことで、難しい問題も解けるようになるのではないかと思っております。
4 ポイント意識
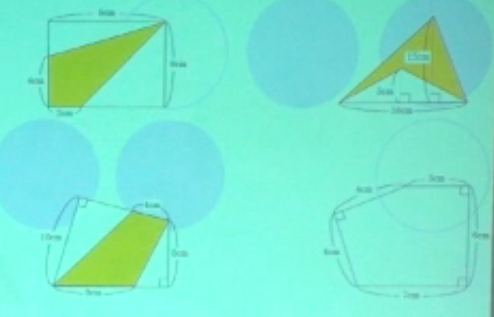
上の図のうち、右下以外の3つはオレンジの部分の面積を求める、そして右下はすべての面積を求めるという問題なのですが、ちょっと眺めてみてください。
・左上は、全体から白い三角形を引いても良いし、真ん中で分けてあげて、三角形を2つにしてもよいです。
・右上は、三角形全体から、白い三角形の面積を引けば良いです。
・左下は、全体から引くことが出来ないので、オレンジの部分を分けて2つの三角形にして求めます。
・右下は、分けてあげると、直角二等辺三角形と台形になります。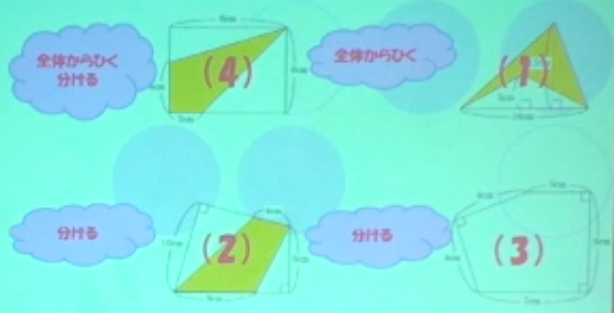
このように、それぞれの図形には「メッセージ」が込められています。
これを上記の順番の通りに解かせるのは、適切ではないと考えます。
例えばこんな順番で解かせてみてはどうでしょうか。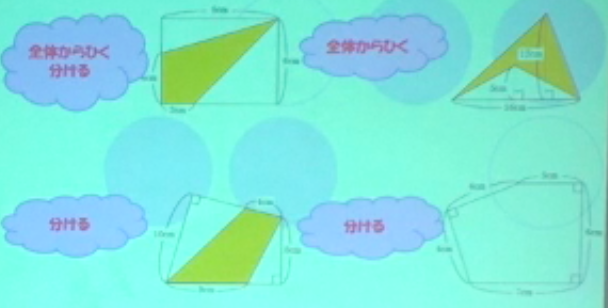
まず「全体から引く」問題を1問やる。次に「分ける」という問題を2問やって、そして最後に分けても全体から引くことでも出来る問題を解かせます。
このように、問題のポイントを意識すれば、どういう順番で問題を解かせるか、ということも見えてくると思います。
5 講師プロフィール
伊藤邦人(いとう くにと)
立命館小学校教諭。
『立命館小学校開校と同時に着任。溢れる情熱で「算数の楽しさ」をこどもたちに伝える。小6担任』(立命館小学校ホームページより引用)







コメント
コメント一覧 (1件)
(1)「同じ条件」と「異なる数値」を使った問題を読みましたが、同意しかねます。
下の問題を解けることを最終目標にするなら、中は上を反復という
点でつないでいても、下の問題のステップにはなっていないのでは
ないでしょうか?
上の問題と下の問題は、引いた数が全部の数になるのか(上)、
1あたりの数になるのか(下)というちがいなのですから、
そもそも難易度が違うのではなく、質が違うわけですよね。
なので、ステップという考え方で解かせるものではないと
考えます。
1あたり量、いくつ分、全部の数の見極めが重要なのですから、
線をひかせるとか、引き算の答えが何になるかというヒントを
予め出しておくという支援がよりふさわしい問題なのではない
でしょうか。
確かに、同じ条件と異なる数値を使うことおが有効な問題も
あるのでしょうが、今回紹介される問題は、それにはふさわ
しくないと考えます。