タングラムで三角形をつくってみよう（シリウス）

2025 8/02

1　はじめに

こちらの記事は、静岡県で30年間以上続く教員サークル、シリウスのホームページに掲載されている教育実践法の一つをご紹介しています。

2　実践内容

タングラムは昔から「知恵の板」と呼ばれるパズルゲームである。七つのピースで影絵を作り出す。一度始めると次々と新しい影絵にチャレンジしたくなる不思議な魅力がある。
この7枚のピースを使って二等辺三角形を作ったり正三角形を作る活動を通して三角形の性質への理解を深めた。子ども達にはまず「タングラム」という知恵の板を紹介した。画用紙に印刷したタングラムを配って指示を出す。

指示1　タングラムで二等辺三角形を作ってみよう。

1. タングラムのパーツから二等辺三角形を見つける
2. 3つのパーツを組み合わせて二等辺三角形を作る
3. 7つ全部のパーツを組み合わせて二等辺三角形を作る

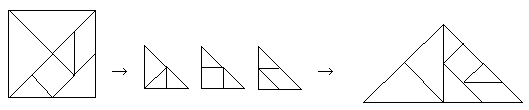
7つのパーツのうち５つが二等辺三角形であることを見つけた。次にそのパーツを使って二等辺三角形づくりに挑戦した。あれこれあれこれやっているうちに「できた」の声。早速前に出てきてもらい、影絵（ＯＨＰ投影機）を作ってもらった。まだできていない子は「むずかしい、むずかしい」と言うので、ヒントを少し影に出したら、ほどなく全員が二等辺三角形を作ることができた。

発問1　二等辺三角形のことを確かめよう。

1. 辺の長さはいくつ同じか
2. 角の大きさはそれぞれ何度か
3. タングラムのパーツには45°の角がいくつあるか

タングラムでの角の大きさは45°45°90°である。よく見ると４５°の角はいくつもあり全部で12個あることが確認できた。

指示2　タングラムを使って今度は正三角形を作ってみよう。

「よーし！」とばかりに挑戦を始めたが、すぐに「できない」「無理」の声。作れないことがすぐにわかったようだ。

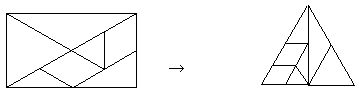
そこでもう一つ別の板「ロングラム」を配った。このロングラムはタングラムを横にルート3倍だけ伸ばしたものである。このロングラムで正三角形ができるかどうかしばらく考えた。

発問2　ロングラムでは正三角形ができるだろうか？

パーツを切り分ける前から〈できる〉と考えた子が多くいた。

〈できる理由〉

・　正三角形は60°だけれど、ロングラムには60°の角がたくさんあるから。

・　ログラムの中に正三角形の形がある。さっきの二等辺三角形も、タングラムの中に二等辺三角形の形があった。

こうした考えを聞いた後もう一度「ロングラムで正三角形ができると思いますか」と尋ねると全員が〈できる〉と考えた。