1 概要
この実践は(株)教育同人社の許可を得て、「はなまるサポート」の学習指導ポイント一覧より転載しています。
実践の続き(無料)は最下部のURLからご覧ください。
また、以下より実践をPDFでダウンロードできます。
http://www.djn.co.jp/support/special/point/docs/2012/1/2/1.php
2 はじめに
ここでは、4年生の算数の「小数×整数」と「小数÷整数」の指導法を見ていきます。また、「小数×整数」では、よく見られる指導例とそれの好ましくない点とそれよりも最適な指導例を含めて見ていきます。
そして、これまでに習ったことをいかに活かして指導したら良いのか?も述べていきます。
対象
小学校4年生
3 「小数×整数」の指導
(1)よく見られる指導例
T,「たろうさんは3L入りのジュースを4本買いました。ジュースは全部で何Lですか。」
T,どんな式になりますか?
C,3×4です。
T,どうして3×4でいいのですか?
C,3Lの4つ分だからです。
C,(1つ分)×(いくつ分)=(全部)の言葉の式にあてはめました。
C,数直線で表すと,

のようになるので,3×4です。
T,そうですね。では,次の問題はどうでしょう。
「たろうさんは0.3L入りのジュースを4本買いました。ジュースは全部で何Lですか。」
T,さきほどの問題とどこが違いますか?
C,3Lが0.3Lに変わったところです。
T,そうですね。では式はどうなりますか。
C,整数が小数に変わっただけなので,0.3×4です。
………
この例では,はじめに既習の整数×整数の場面を取り上げ,そこからの類推によって小数×整数のかけ算の立式をさせています。しかし,これはあまり好ましいものではありません。その理由は次の通りです。
–
1. はじめに整数×整数を取り上げることは,明らかに次の立式を示唆している。これでは次の演算決定を予告されているようなもの。
2. 整数×整数から小数×整数を類推しているように見えるが,これは,「類推させられ」ている。
3. 立式の根拠が,整数×整数の場合を扱っているのみである。
ここでは,次のような展開が望ましいのです。
–
1. はじめから小数×整数の問題場面を取り上げる。そして,児童が前に学習した場面と同じところはないか,違うところは何かを明確にしようとするように助言する。
2. 理解が遅い子には「もし,この小数のところが整数だったら…」と助言し,そういう見方(単純化の考えの1つ)を育てる。
3. その上で「整数のときは整数×整数だったから,小数の場合も小数×整数でいいのではないか」と児童自らが類推できるようにする。
4. そして,本当に小数×整数でよいか,言葉の式や数直線による数の関係から立式の根拠を明確にする。
これは,かけ算の場面に限りません。わり算の場面でも同じように扱う必要があります。
(2)小数×整数の計算方法のまとめについて
1. 基本的には,0.1を単位として,そのいくつ分かで計算します。
- 下位単位を用いる場合は,3.5L=35dL
- 0.1を単位とする見方では,3.5は0.1が35こ
2. 3.5は0.1が何こかを表すのは,3.5×10=35
3. 0.1が35をもとにもどすには,35÷10
4. 例えば,3.5×9=3.5×10×9÷10(10倍して整数に直し,答えを10で割って0.1の単位に戻す)
5. 「一般に,小数×整数は小数を整数に直して計算してから答えを小数に直す。」とまとめる。
この考え方で,筆算もできることを確かめ,被乗数が小数第二位,第三位のばあいまで拡張します。
4 小数÷整数の指導
(1) 小数÷整数の演算決定について
この場合も,小数×整数の場合と同じように,数直線や言葉の式で演算決定しますが,整数×整数の場合からの類推だけで終わらせないようにしましょう。また,計算の仕方の都合から等分除の場面を取り上げることが多いが,演算決定に当たっては,等分除,包含除の両方を取り上げて正しく立式させる必要があります。
①等分除の問題場面
T,次の問題をしましょう。
「7.2Lの牛乳を4人で等分します。1人分は何Lですか。」なに算になりますか?
C,わり算です。
T,どうしてわり算だと言えますか?
C,数直線から
□×4=7.2 で
□=7.2÷4 です。

C,言葉の式で,1人分=全部の量÷いくつ分だから7.2÷4です。
②包含除の問題場面
T,次の問題をしましょう。
「1Lで3㎏の砂があります。9.6㎏では何Lですか。」なに算になりますか?
C,わり算です。
T,どうしてわり算だと言えますか?
C,数直線から
3×□=9.6で
□=9.6÷3です。

C,言葉の式で,いくつ分=全部の量÷1つ分だから9.6÷3です。
また,包含除の「何倍」の扱いで小数÷整数の場面については,単元内で特設して扱うので,例のような場合について演算決定では触れておくとよいでしょう。
(2)小数÷整数の計算方法について
小数÷整数の計算方法を考える上で,子どもたちの既習事項になるものは,「小数×整数」の学習で得た事柄です。すなわち,
- 小数の整数化
- 3.5×9=3.5×10×9÷10(10倍して整数に直し,答えを10で割って0.1の単位に戻す)
- 下位単位に直して整数化する
- 0.1のいくつ分かと考えて整数化する
そうすると子どもたちは次のように類推するでしょう。
- わり算も小数を整数化すればよさそう。
- 7.2÷4=7.2×10÷4÷10にすればいいのではないかな。
- かけ算の時は,0.1を単位にして考えたからこの場合も同じように考えるといいのではないか。
1. 0.1を単位にした表し方に直して計算する
- 7.2Lは,72dL。だから72÷4=18これは18dL=1.8L
- 7.2は0.1が72個。だから72÷4=18これは0.1が18個だから1.8。
2. 10倍したから10でわる計算をする。
- 7.2÷4=7.2×10÷4÷10(なぜこの式でよいか説明が必要) =72÷4÷10 =18÷10
=1.8
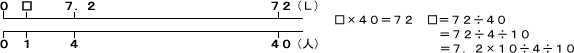
3. 7.2Lを7Lと0.2Lに分けて考える。
7÷4=1あまり3 3.2Lを32dLと考えて32÷4=8
8dL=0.8L だから,1Lと0.8Lで1.8L(これはわり算の概算につながる方法)
(3) 小数÷整数の筆算
子どもたちは整数÷整数の筆算の仕方は理解しているのですから,「小数÷整数の計算は小数を整数に直して計算すればよい」という考え方から類推すれば,整数に「小数点を外して整数のままで計算して,あとで小数点をつける」と考えます。そして実際のわり算は「わり算の筆算のアルゴリズム」に従って,「たてる,かける,ひく,おろす」のように処理します。この流れのままでよいのでしょうか。
「計算の仕方」で小数を整数に直して計算すればよいと学んでいるのですから,子どもたちは,整数÷整数の筆算をするのは当然のことです。問題は,「商」や「あまり」の処理です。すなわち,
1. 商のどこに小数点をうてばよいのか。それはなぜなのか。
2. 「あまり」で出たらどこまで割り進むのか。また,「丸める」のか。
3. 「あまり」を表すにはどこに小数点をうつのか。
などを明確に指導することが大切です。
①-1 7.2÷4の概算から考える。
・まず7.2を7と考え 7÷4 をする。
これは4×□=7の□を求めること。
□=1にすると4×1=4
□=2にすると4×2=8 なので
□=1
そこで,7.2−4=3.2 の3.2で3.2÷4をする。
これは,0.1を単位にして考えて
32÷4=8 だから3.2÷4=0.8
だから求める答えは,1+0.8で1.8
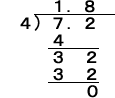
①-2 7.2を72と見て,整数÷整数の筆算をする。
・72÷4の筆算をアルゴリズムに従ってする。
72÷4=18になる。
18は,0.1が18個なので1.8のように小数点をうつ。
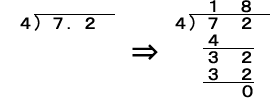
※①と②では筆算としてはどちらが「簡単,簡潔,明瞭」であるか,さらに整数÷整数の筆算との区別も考え,①の方法にまとめていく。
②-1 わり進むことと丸めること
T,次の問題をしましょう。
「2.7Lのジュースを6人で完全に同じように分けると,1人分はどれだけになるでしょう。」
T,式を書いて計算して答えを求めましょう。
C,2.7÷6=0.4 あまり0.3
答え0.4Lずつで0.3Lあまります
C,「完全に分ける」のだから,あまってはいけないと思います。
T,では,どのようにしますか。
C,のこりの0.3Lも6等分します。
C,0.3÷6の計算は,0.1を単位にすると3÷6でできないので,0.01を単位にします。
すると0.3は0.01が30個なので30÷6=5 0.01が5個で0.05です。
C,だから,0.4Lと0.05Lで0.45Lです。
T,では,このことを筆算にしてみましょう。
(と言って,わり算の筆算形式をCの説明と対比させながら整理していく。この場合のポイントは,「割り進む」必要性から指導することである。)
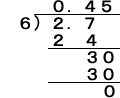
5 実践の続き
続きは以下のURLをご覧ください。
http://www.djn.co.jp/support/special/point/docs/2012/1/2/1.php
6 実践者紹介
初等教育研究所
山﨑 憲
【プロフィール】
元東京都算数教育研究会会長。
「小学校時代から現在までで,今が最も算数がすき」と,小学校退職後も算数教育に没頭し,現職時代に引き続き年に数回研究授業も試みている。
現在東京学芸大学講師として初等算数科教育法を担当。またボランティアとして東村山市算数教室を開催し算数好きの子どもの育成を目指している。
7 サービス紹介
同社の「はなまるサポート」は、若い先生のための授業ヒント集として、毎月の学習指導ポイントを細かく解説したり、不明点や疑問点などに関する無料相談を受け付けたりしています。
8 編集後記
「整数×小数」を教える際、はじめに整数×整数を取り上げることが好ましくない理由を知って、とても腑に落ちました。初めての計算であっても、まずは児童に考えさせることの重要性を改めて知れた実践であり、それこそが児童に深い理解をもたらす要因なんだろうと思います。
(編集・文責:EDUPEDIA編集部 岸剛志)





コメント