1 掲載経緯
東京女学館小学校の小野寺美賀先生は2009年5月25日付けの朝日新聞の「花まる先生公開授業」 で紹介されました。それをきっかけとして、取材を行い、資料を提供してくださいました。本稿は提供して頂いた小野寺美香先生の資料のうち、場合の数の授業の意図を紹介します。なお、提供資料は文末よりダウンロードください。
2 授業の意図
「みんなは何が好きか」というのは、だれしも興味深いものである。さらに自分と同じものが好きな人はいるのか?自分と同じでない人はどのようなものが好きと感じているのか?果たして何通りの答えがあるのか?…そのような児童の興味・関心、知りたい気持ちを利用して、算数が苦手な児童にも楽しんで学ぼうとする授業を試みた。難しいと思われる数式も実際に友達の考え方を聞き、その考え方を整理することによって導き出せるようにする。順列の数式を導く思考は樹形図によって引き出され、組み合わせは表によって考えると導きやすいことを知る。この授業の面白さは、順列の場合の数の増え方である。2種類のときは2通り、3種類のときは6通り、4種類のときには24通り、5種類のときには120通りというように、並べるもの(選択肢)が2種から5種類に、たった3種類増えただけで、場合の数が118通りも増えるのだ。
6種類で720通りまで考えた後、10種類になったらどうかと考えさせる。まさか、3628800通りとすぐに考える児童はいないだろう。選択肢が7種類になったときの場合の数まで学習した後の児童は、だれしも当てずっぽうで答えることはしない。計算して正しい数を求めたいと思うようになる。また、樹形図や表を利用することにより数式の意味も理解できる。実際に友達全員の話(好きな順番)を聞くこと(や)、すべての組み合わせを樹形図であらわすことは面倒なことであり、効率的ではない。この授業では、数の増え方の規則性を表や求め方から見つけて、数式を導き出すことは有効であることに気付かせることができる。そこから、数学的な考え方の面白さ、便利さが伝わればよい。
–
順列学習後、同じ食べ物を利用して組み合わせの学習をする。女学館ならではの体育活動であるリトミックの組み合わせが何通りあるのかを知り、自分達が行っている活動の素晴らしさに気付くのもよい。
サイコロ遊び:
さいころを2回振ります。何通りの目の出方が考えられますか?3回、4回と増やしていくとどうなるかなど自分で場合の数を使って解く問題を考え、樹形図や表から数式が導き出せると思うと算数が楽しくなる。さいころを3回振って3回とも同じ目の出る確率はどれくらいなのか(6×6×6)分の6を計算してみた後、実際に3回とも同じ目が出るまでさいころを振って遊んでみるのもよい。確率が36分の1であることは、36回行ったときに必ず1回起こるとは限らないところもおもしろい。それが確率。発見する喜びは、どの教科においても楽しさの必要条件である。そして、「これはどうなるのか?」次の課題が見つかるように指導し、楽しさが増すようにしていきたい。
–
豊かさがもたらしたもの、手で労働することを嫌がる、面倒がる児童が増えている。何でも楽なものばかり与えられていると、脳が鍛えられない。考える道筋、思考の仕方を図や表に書き表すことは重要である。初めから与えられた効率的な考え方ではなく、自らの力で導き出すことが重要。「急がば回れ」から身につくことは多い。
あえて面倒な作業をさせることによって、自分から効率良くする工夫、数式を常に考えるようになる。小学校教育では与えられた数式を覚えることではなく、時間はかかっても自分で数式を導き出すことを重要視して授業を組み立てている。
注釈:「場合の数」は、学習指導要領の改訂により6年生の指導事項から削除され、現在は中学2年生の単元ですが、女学館小学校では現在も6年生で指導しています。
提供資料はこちらからダウンロードして下さい。
資料1(指導案)「場合の数指導案」(Word:47KB)添付ファイル
資料2(教材)「算数探検隊 場合の数・順列」(Word:54KB)添付ファイル
資料3(教材の使用例)
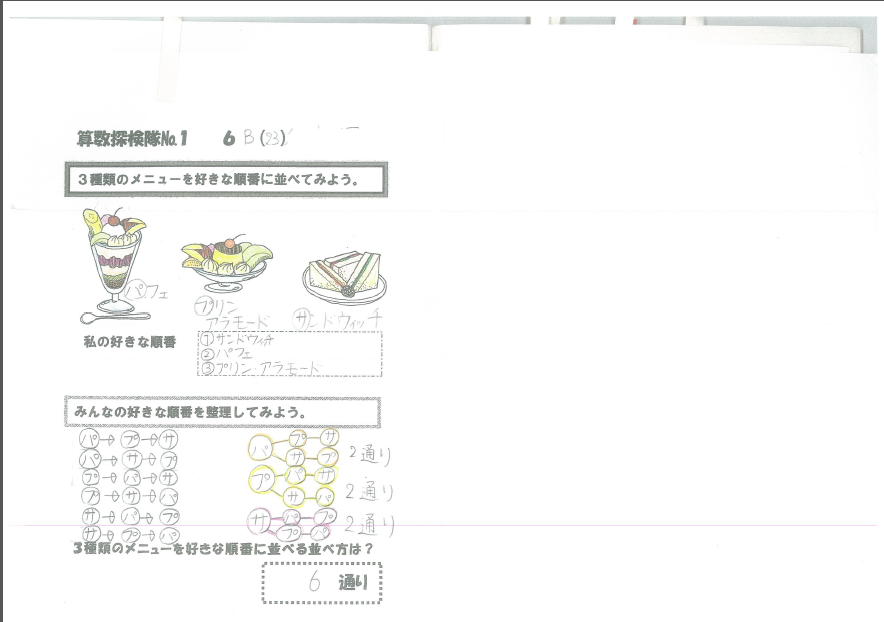
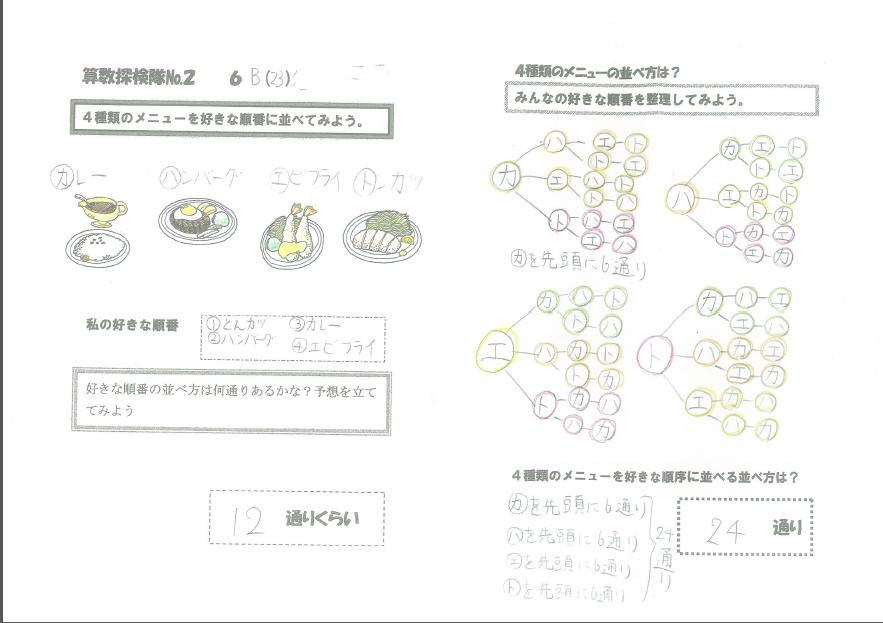




資料4(イラスト)(PDF:276KB)添付ファイル









コメント
コメント一覧 (1件)
取材時に伺ったところ、ケーキでなくても他の食べ物や動物、児童に人気の芸能人(5人組の嵐など)を代わりに当てはめるように工夫をすると、より反応が良くなるという事例もあるそうです。