1.1 はじめに
この単元は,6年間の算数の学習のまとめとしての特設単元である。
児童が今までに学習してきた内容を元に自分たちで問題を作成し,問題の解法を考え,算額に表すことで数学的表現力を育てることを目的としている。単に問題を繰り返し解くだけではなく,学んだことを活かして自分で考え,表現する機会を作ることで理解を深めることが出来,教師の働き掛けにより学習内容の定着へと導くことの出来る間嶋哲先生の実践を紹介したい。
1.2 間嶋哲先生の授業例
※2022/07/03現在 閉鎖。
単元名 数学的コミュニケーション広場で,算数博士になろう!
—『算額』(算数の絵馬)をつくろう—
本単元で高める力
数学的表現力を高める。
具体的には,次の3つの知を獲得させる。
1.3 指導の構想
本単元は,小学校六年間の総まとめとしての特設単元である。 一人一人に『算額』を作らせる活動が中心となる。

上の算額は,羽黒山に奉納されているものである。
『算額』とは,江戸時代以降,人々が和算の問題を考えたり解けたりした時に神社や寺に奉納した絵馬のようなものである。その算額には,自分で作った問題と,その解法が漢文調で書かれている。
つまり,算額には,「問題づくり」と「解法」という二つの要素がある。実際に算額の問題を解くためには,中学生以上の数学の知識を必要とするものがほとんどである。しかし,あえて算額作りをさせる。その理由は,下記の3点である。

「問題づくり」を次のようにさせる。
1. 算額の内容や歴史的な背景を話し,「6年間のまとめ」として,「問題づくり」をすることを提案する。
2. 「どんな問題をつくったらいいのか。」様々な意見を出させ,イメージを膨らませる。その中で,例えば「良い問題」が,具体的にどのような問題なのか明確になる。
3. まず,自分でつくってみる。すると,自ずと,これまでの教科書や自分が使っている参考書などを持ち込むことが想定される。
4. つくってみたら,近くの友達に出題してみて,感想や意見を聞き,改善していく。
5. どうしても問題づくりが困難であれば,既成の問題を参考にしてもよいことを補足する。
数学的表現力を育てるために,それぞれの問題づくりが終わり,互いの問題を解き合う段階で,以下に示す働き掛けを行う。

自分が選んだ問題を『細分化カード』を使って解かせる。なお,『細分化カード』とは,次のようなカードである。(実際のカードは,研究紀要を参照)

子どもは,『細分化カード』で自分の解法を,次のように表そうとする。
「図・表エリア」…問題の全体的な構造を図に表したり、解決の糸口を表に表したりする。
「言葉・式エリア」…解決までの過程を、筋道に沿って3つに分けて表したり、言葉/式が適切かを検討したりする。
その際,内容知を獲得する子どももいる。 『細分化カード』に,解法をかいた子どもに,次の働き掛けを行う。

できた『細分化カード』を,黒板前の「数学的コミュニケーション広場」にもっていき,掲示させる。外の友達に評価してもらうためである。
–
評価の際は,正しく解法が伝わるかどうかという観点で,○か△を付けさせる。
○とは,その解法が説明できるという意味である。
△とは,うまく説明できないという意味である。
最後に,全体的な評価を言葉で書き込ませる。
このような相互評価を行うことによって,カードの数学的表現が,相手に正しく伝わるのかどうかを試すことができる。また,友達の数学的表現も評価するので,体験知を獲得する場合もある。評価された子どもは,解法のどの部分が相手に正しく伝わらないのか,自覚することができる。そのような子どもに,次の働き掛けを行う。

これによって,子どもは,自分の解法を「相手に正しく分かってもらえる表現」に高めることができる。 ここで,子どもは,想定した方法知を獲得する。また,全員が内容知を獲得する。解法を創り出し,内容知と方法知を獲得した子どもに,次の働き掛けを行う。

これによって,子どもは自分の視覚的表現の高まりを自覚し,成就感や満足感を味わう。この段階で,子どもは,想定した体験知を獲得する。
そして,次に行われる全体での比較検討の場で,自信をもって発表したり,比較検討したりしようとする。なお,この場合の比較検討は,有効性の検討のみである。すでに一連の働き掛けを通じて,妥当性の検討と関連性の検討は終わっているからである。
1.4 指導計画 全21Q〈7時間〉


1.5 本時の構想
《一日目》 (10~13/21Q)
(1) 主眼
2つのグループに分かれて,それぞれの問題を解き合い,解決方法を細分化して表し,その表現方法を相互評価し合う活動を通して,論理を表す式と「とすると」「だから」「つまり」などの論理をつなぐ言葉が分かる。
(2) 展開
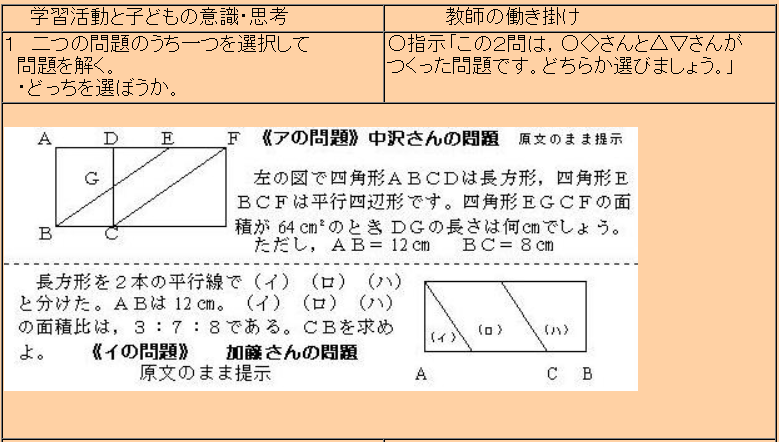



(3) 評価
一連の働き掛けによって,論理を表す式と「とすると」「だから」「つまり」などの論理をつなぐ言葉が分かる。
《二日目》 (14~17/21Q)
(1) 主眼
小グループに分かれ,他のグループの問題を,解決方法を細分化して解き合い,その表現方法を相互評価し合う活動を通して,これまで自分で使わなかった数学的表現に気付いたり,これまで使わなかった数学的表現を付け加えたり,自分では気付かなかった数学的表現のよさを感じたりできるようにする。
(2) 展開

(3) 評価
一連の働き掛けを通して,これまで使わなかった数学的表現を自分の解決方法に使ったり,自分では気付かなかった数学的表現のよさを感じたりできる。
1.6 編集後記
学習内容を理解した後にオリジナルの問題を作成し,解法も自分自身で作成する作業を通して体験に基づいた知識を得ることが出来ると感じました。そのことにより学習内容の理解を深め、定着させる効果が期待されます。また,自分が得た情報を自分なりの表現で発信するという経験は算数の学習に留まらず,様々な場面で役立てることが出来ると考えます。授業の成り立ちにおいて間嶋先生の実践は教師の適切な働き掛けが軸となっているのだと感じました。
(編集・文責:EDUPEDIA編集部 山口珠歩)
1.7 講師プロフィール
間嶋 哲(Mazima Akira)
1965年,新潟県に生まれる。新潟大学教育学部を卒業。
新潟県内の小学校で活躍後,文部科学省での1年間の研修を経て,現在,新潟市教育委員会学校支援指導主事。算数授業ICT研究会理事。全国算数授業研究会総務幹事。趣味は,海外旅行・外国語会話・スキー・ギター(フォークとクラシック)・読書・園芸・熱帯魚飼育など,多岐に渡る。
大学の卒業旅行を機に,旅行・外国語にはまり,旅行記を一冊出版したほどのエピソードを持つ。
–
●HP 間嶋哲のHPへようこそ… http://bit.ly/homepage_majima
※2022/07/03現在 閉鎖。









コメント