1 概要
この実践は(株)教育同人社の許可を得て、「はなまるサポート」の学習指導ポイント一覧より転載しています。
実践の続き(無料)は下部のURLからご覧ください。
また、以下より実践をPDFでダウンロードできます。
添付ファイル
1 この学習の到達点
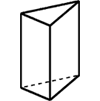
上のような三角柱の体積を求める学習の到達点はどのようなことでしょうか。それはおよそ次のようです。
- 周囲のある三角柱(具体的な形)を認識しその体積を求める方法を考え、公式化しようとすること。
- 三角柱の体積の求め方について、直方体、四角柱の体積の求め方から類推し、図や式を用いて考え、表現すること。
- 三角柱の体積を、公式を用いて求めることができること。
- 三角柱の体積は、底面積×高さにまとめられることを理解すること。
- 三角柱の体積の求め方を利用して、他の角柱の体積も「底面積×高さ」で求められることを一般化しようとすること。
中学校の1年生では、小学校で「柱体の体積=底面積×高さ」が理解されているものとして指導が展開されます。また、柱体そのもののとらえ方も「立体図形」(小学校)から「空間図形」(直線や平面の移動によって構成された図形)と見るようになります。すなわち、三角柱は底面の三角形がその高さ分だけ平行移動した空間図形という認識の上に立ち、「柱体の体積=底面積×高さ」とするのです。
以上のことを理解して、小学校における指導に当たる必要があります。
2 どのような既習事項をどのように活かすのか

上のような三角柱の体積を求める問題の解決には、どのような既習事項が必要とされるでしょうか。
大切なことは、求積の問題解決の過程が、面積の場合と同じように考えられないか、もし考えられそうだとしたら面積の場合から類推して考えられないかという態度で臨めるようになることでしょう。そこで、次のように整理してみました。
(1)四角柱の体積の求積
四角柱の体積は、直方体の求積公式からの変形と、求積の原理である1cmのいくつ分かで表すことが基本です。
① 「1cmのいくつ分か」の考えから、高さ1cmの板の何cm分かを考える見方です。

この時に、高さが1cmの直方体の体積と、底面の面積は数値が同じになることに着目させます。すなわち、求める体積=「底体積」の3倍、つまりこの場合は20cmの3倍となりますが、高さが1cmなので、数値としては底面積(20cm)を表す数値「20」と同じになります。そこで、四角柱の体積=底面積×高さと見ることもできると理解させます。
② 直方体の体積=たて×よこ×高さの公式から、図のように

そして、①、②の両方から
四角柱の体積=底面積×高さ
と見ることができることをまとめるのです。
(2)三角形の面積の等積変形、倍積変形による求積
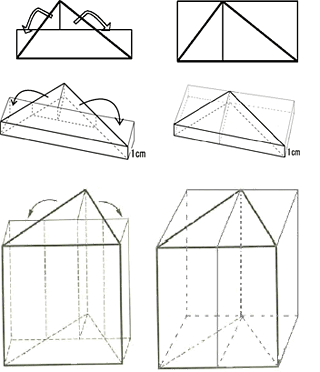
これらは、いずれも「習った形」(長方形)に直して考えるというアイディアです。このことを底面が三角形の柱体の「底体積」に応用していくのです。
また、上のように立体そのものを平面図形の場合と同じように、体積の等積変形や倍積変形していきます。その際、子どもたちの理解を助けるために、実際の模型を発泡スチロールなどで作り、それと対比させながら変形のアイディアを説明できるといいと思います。
そして、これらはいずれも四角柱に変形されたわけですから、変形された部分がもとの三角柱のどの部分に当たるのかを考えて立式していくのです。
「柱体の体積」の指導~既習事項を活用した類推の仕方~②(はなまるサポート) | EDUPEDIA
3 実践者紹介
山﨑 憲
元東京都算数教育研究会会長。
「小学校時代から現在までで,今が最も算数がすき」と、小学校退職後も算数教育に没頭し、現職時代に引き続き年に数回研究授業も試みている。
現在東京学芸大学講師として初等算数科教育法を担当。
またボランティアとして東村山市算数教室を開催し算数好きの子どもの育成を目指している。
4 サービス紹介
同社の「はなまるサポート」では、若い先生のための授業ヒント集として、毎月の学習指導ポイントを細かく解説しています。また、不明点や疑問点などを無料で相談を受け付けています。
(編集・文責:EDUPEDIA編集部 佐藤 睦)









コメント