1 概要
この実践は(株)教育同人社の許可を得て、「はなまるサポート」の学習指導ポイント一覧より転載しています。
実践の続き(無料)は最下部のURLからご覧ください。
また、以下より実践をPDFでダウンロードできます。
http://www.djn.co.jp/support/special/point/docs/2011/7/2/plan.pdf
2 はじめに
5年生の指導で、整数×小数では、「小数倍」の指導とか、かけ算の意味の拡張とか言われます。そして、「小数倍の指導では数直線が有効なんだ」とも言われています。先輩の先生からもそのような話を聞いた方もいらっしゃるでしょう。今回はそのことを取り上げます。
ところで、この「小数倍」の指導のところで、実際に指導してみたあなた自身がすっきりしないと感じているところがありませんか。次の問題場面を例にして、曖昧なところをすっきりさせましょう。
3 内容
そこで、まず既習の場面を想起させてみましょう。
=== 1m80円のリボンがあります。ひろき君は2m、さとし君は3m買います。
それぞれいくら払えばよいでしょう。
ひろき君の場合
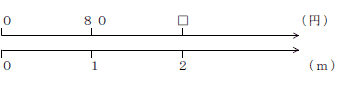
数直線で長さと値段の関係を表すと、上のようになり、□=80×2で求められます。
だから式は、80円の2倍のかけ算で表されます。これは既習事項です。
さとし君の場合
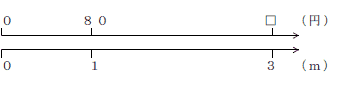
数直線で長さと値段の関係を表すと、ひろき君同様、上のようになり、□=80× 3で求められます。だから式は、80円の3倍のかけ算で表されます。これも既習事項です。
ひろき君の場合もさとし君の場合も、数直線上の数の位置関係が同じであり、これは「かけ算」の演算を表す位置関係です。
ここまで確認した上で、すずえさんの場合を数直線に表してみますと、
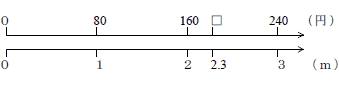
のようになります。これは、ひろき君とさとし君の場合も一緒にした数直線です。
まず、2m、3 m の場合にはそれぞれ160円、240円ですから、2.3mの場合も確かにその間に値段があることが分かります。また、2.3のように小数の場合も数直線に表したとき、乗数が整数の時と同じような位置関係になっていることから、「かけ算になるのではないか」という類推が働きます。
そこで、この場合もかけ算を用いることにしようと意味を拡張するのです。
これは、言わば「約束」です。子どもが「見つけられるきまり」ではありません。
よく、80×3.5って書いたっていいんだよ。だって3.5個分と言っても意味が分かるじゃないかと言う子ども(先生)がいますが、それはおかしなことです。なぜなら、これまでのかけ算は、80×3なら、80+80+80のように同数累加で定義してきたのです。80×3.5は80の累加、つまり80のたしざんでは表せません。
ですから、ここで新たに3.5倍のように小数倍の場合を含めて80×3.5と書いてもいいことにしようと決め直すのです。
従って「なに算になりそうですか。それはなぜそう思うのですか。」「かけ算になるとして、どんな式にしましょうか。」と発問して、子どもの類推を参考にしたようにして、80×2.3を定義するのです。
このように、80×2.3は,子どもたちに「見つけさせる内容」ではなく、「教える内容」です。しかし、単に「教え込む」のではなく、子どもたちの既習を生かして新たに定義していく展開が望ましいですね。
実践の続き
続きはこちらからご覧ください。
http://www.djn.co.jp/support/special/point/docs/2011/7/2/2.php
4 実践者紹介
初等教育研究所
山﨑 憲 プロフィール
元東京都算数教育研究会会長。
「小学校時代から現在までで,今が最も算数がすき」と、小学校退職後も算数教育に没頭し、現職時代に引き続き年に数回研究授業も試みている。
現在東京学芸大学講師として初等算数科教育法を担当。
またボランティアとして東村山市算数教室を開催し算数好きの子どもの育成を目指している。
5 サービス紹介
同社の「はなまるサポート」では、若い先生のための授業ヒント集として、毎月の学習指導ポイントを細かく解説をしたり、不明点や疑問点などを無料で相談できたりします。
http://www.djn.co.jp/support/
(編集・文責:EDUPEDIA編集部 阿部由和)









コメント