円でイメージさせる。
分数が算数の躓きはじめだったという子供はけっこう多いです。4分の1程度の簡単な分数でもイメージしにくいようです。
イメージがしにくい原因のひとつは、「1」「もとになる数」、あるいは「全体」が、何であるかがはっきりしないという、子供たちにとっての不全感があるのではないかと思います。「リボンの『3分の1』」と言っても、「1mのリボンの『3分の1』」と「1.5mのリボンの『3分の1』」では違った数です。また、
「3分の1」>「4分の1」
というのも、しっかりと分数の意味が把握できていない子供にはピンときにくいのではないでしょうか。
・
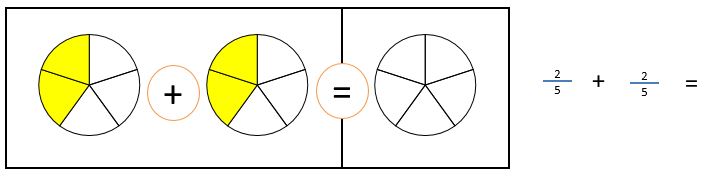
円は「1」が見えやすい形です。上図のように「5分の2」を表すと、視覚的にとらえやすくなります。たくさんの分数を円で表したファイルを添付しているので、ぜひ、色を塗らせて使ってみてください。
実際に色を塗ってみることで、分数の意味が感覚的に分かってくると思います。こうしていくと、
「3分の1」<「4分の1」
というように、分母の大きい方が大きいという勘違いをしにくくなるのではないでしょうか。
・
□つに分けたうちの一つ
分数は全体をいくつかに分けたうちのいくつかである。だから、「3分の1」は全体を「3つに分けたうちの1つ」ということになります。分子が「1」である分数、「□分の1」というのは、一つの単位であるように考えればいいでしょう。分子が「1」である分数を単位分数といいます。
●「3分の2」は「3分の1」が2つあることだよ。
●「5分の3」は「5分の1」が3つあることだよ。
●「4分の7」は「4分の1」が7つあることだよ。
こうして円を「1」として、分数を単位分数の集まりだというとらえ方に慣れさせていけば、子供たちも少しは納得して分数をとらえることができるようです。
・
通分や約分の学習をする時にも、円でイメージさせると理解の助けになると思いますので、下記↓のページをご参照ください。
・
分数を円でイメージさせる(算数3~6年生)【教材】
分数には2つの意味があります ~5年分数【教材】
約分・通分を円で理解する ~5年生分数【教材】







コメント