1 はじめに
2016年8月9日火曜日に行われた伊丹市中学校数学科夏季研修会を、EDUPEDIA編集部が取材しました。この研修会では、伊丹市内の中学校の数学の先生と市教育委員会指導主事の先生等が約40人集まり、先生方の活動報告、そして若手教員による模擬授業とそれに対する意見交換が行われました。
前編となる本記事では、正負の数の減法と証明問題について、2人の先生の模擬授業と意見交換の模様をご紹介いたします。
後編では関数の導入(中1)と因数分解についてご紹介いたしますので、あわせてご覧ください。
記事はこちら⇒「関数の導入(中1)・因数分解の指導法~伊丹市中学校数学科研修会での模擬授業を通して<後編>~」
2 若手教員による模擬授業
研修会では、合計4人の若手教員による模擬授業が行われました。伊丹市中学校数学科研修会は長く執り行われていますが、模擬授業を組み入れるのは今回が初めてだそうです。若手教員がどのように教えたらよいか悩んでいる箇所を投げかけ、他の先生と意見交換をすることを目的としています。1人の先生の持ち時間は、簡単な模擬授業の約5分間と、それに関する意見交換が20分程でした。
3 A先生の模擬授業 ~正負の数の減法~
授業内容
(+8)−(+5)=(+8)+(−5)であること、つまり「+5を引くことは-5を足すことと同じである」ということを、数直線を利用して指導する。
困っていること
中学校1年生で正負の数の加減乗除を習います。小学校までとは違って負の数の概念が必要となったり、引き算を負の数を足すことと捉えることが要求されたりするため、中学数学の最初のつまずきポイントとなっています。
A先生は教科書にある数直線を用いて正負の数の減法を生徒に説明しようとしましたが、どうしてもわかりにくくなってしまい、他にわかりやすい説明の仕方と、見てわかりやすい説明図の工夫について助言を求めたいとのことでした。
— A先生の授業の流れ
まず、授業の導入で、小学校の学習内容を持ち出します。
□+5=8
という式を提示し、「□に入る数字はなんですか?」と発問します。
そこで「3!」という反応があれば、「どういう計算式で3になるか」という質問をし、
8-5=□
の式を得ます。
次に、(+8)−(+5)の式について、数直線を用いて考えます。
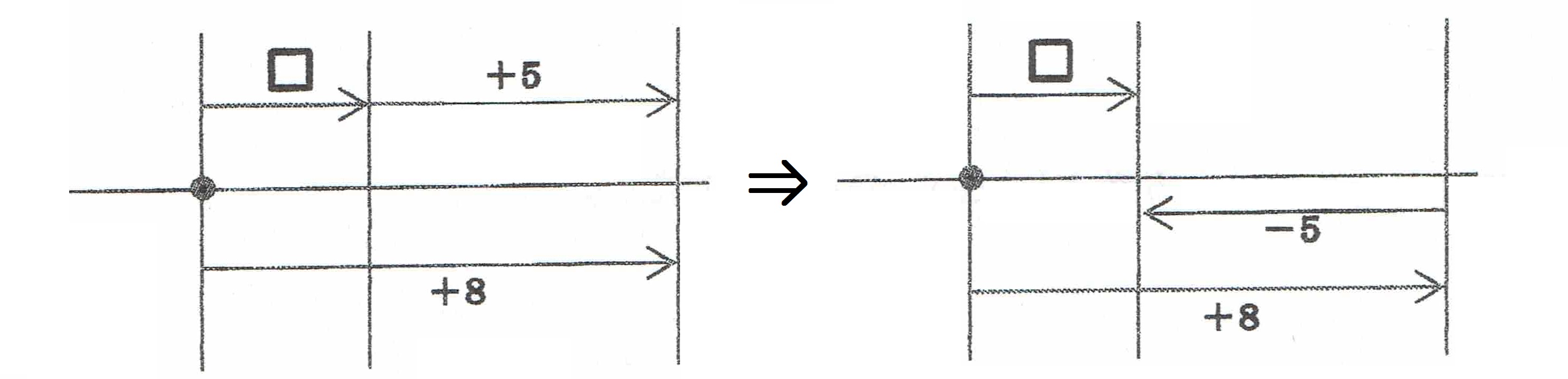
左の図は「答え(□)と+5を足せば+8になる」を示す数直線で、導入で生徒たちに考えさせた式変形から得られます。そこから、図を右図のように変形させ、同じ□を求める式として、(+8)+(−5)が導けるという指導です。
ただ、この指導が有効か、自分でも自信がないということでした。
A先生に対する助言
— 教室を歩いて説明する
プラスを東向き、マイナスを西向きに歩くとして説明するという意見が最初に出ました。実際に+8は教室を東に8歩歩きます。引き算の時は西向きに歩きます。
例えば、(+8)−(+5)であれば、
「東に8歩、西に5歩歩きました!先生ははじめの位置から東に何歩のところにいますか?」
といった発問をします。
すると、「東に3歩!」という反応が返ってきて、答えの+3を導くことができます。
そして、(+8)+(−5)のときは、
引き算のように西向きに5歩歩くのではなく、足し算の時の進行方向である東を向いたままムーンウォークで東から西へ5歩戻るというパフォーマンスをします。この先生の授業中のムーンウォークは生徒の心をつかむようです。
導入からしばらくの間は、
- 符号+を「前進」
- 符号−を「後退(ムーンウォーク)」
- 足すを「東向き(に進む)」
- 引くを「西向き(に進む)」
に置き換えて、楽しませながら授業を行うという提案でした。
— 言葉遊びで説明する
言葉遊びを用いて説明するという先生もいらっしゃいました。
例えば、「身長が5㎝縮む=身長が−5㎝伸びる」
「5万円の赤字=-5万円の黒字」といった具合です。
こうした例から、マイナスが付くと言葉が逆になるということを理解してもらい、
「5を引く=-5を足す」まで話を持っていくという指導の提案でした。
— 「貯金」「借金」で説明する
また、貯金と借金という言葉を使う例もあります。例えば、
(+8)−(+5)
は、「貯金8から貯金が5減った」
(+8)+(−5)
は、「貯金8に借金が5増えた」
(+8)−(−5)
は、「貯金8から借金が5減った」
という具合です。
「借金が減る」ということは、うれしいことだという認識から、自分にとってプラスの情報、すなわち負の数を引くとプラスになるということを理解してもらいます。
— トランプを使って説明する
班でトランプゲームをします。トランプの黒と赤を利用したゲームで、ババ抜きに似た形で行います。
~置き換え~
足す:友達からカードを1枚とってくる
引く:友達にカードを1枚もらってもらう
+:黒(クローバー・スペード)
−:赤(ダイヤ・ハート)
ex)クローバーの2やスペードの2…+2 ダイヤの2やハートの2…-2
そして、手持ちのカードの総和を計算します。
1. 足し算の指導…カードをとってくる
(例)
手持ち:スペード3・クローバー7・ダイヤ8
取ってきたカード:スペード2
→ 3+7+(-8)+2=4
手持ち:スペード3・クローバー7・ダイヤ8
取ってきたカード:ハート2
→ 3+7+(-8)+(-2)=0
2. 引き算の指導…カードをとってもらう
(例) 「+6-(-4)をやってみよう!」
手持ち:クローバー6・スペード4・ダイヤ4
(→ 6+4-4=6)← 手持ちの総和が”6”になるセット
取ってもらうカード:ダイヤ4
→ 手元に残るカード:クローバー6・スペード4
→ このとき、手持ちのカードの総和は、6+4
⇒「カードゲームで+6-(-4)をやったら、6+4になったね」という声かけで、
「+6-(-4)と6+4は一緒!」と結論づける。
よりイメージをしやすくするため、「赤色をとってもらったら手持ち増えて得するよね」と声をかける。
3. 掛け算の指導(番外編)
(例1)「‐2×3」
ダイヤ2またはハート2のカードを3枚もらう
⇒赤色の手持ちカードが増えて、総和がとても小さくなることで、
‐2×3の答えが負であることをイメージさせます。
(例2)「‐2×‐3」
スペード6またはクローバー6と、ダイヤ2またはハート2のカードを3枚をもっておく(手持ちの総和が0の状態)。
ダイヤ2またはハート2のカードを3枚とってもらう(手持ちの総和が6になる)。
⇒「赤色のカードをとってもらうと手持ちのカードの合計が増えて得するね」と声をかけ、
‐2×‐3の答えが正であることをイメージさせます。
まとめ
同じ問題に対して、数学的なもの、国語的なもの、さらにはゲーム的なものまで、複数のアプローチがあります。数式だけを使用した方がわかりやすい生徒と、抽象的な数式を具体例にあてはめて教えたほうが理解できる生徒とがいるのは当然です。限られた授業時間内で生徒にわかりやすく教えられるよう、一つの問題に対して複数の観点からの説明を用意しておくべきだと感じました。
4 B先生の模擬授業 ~証明問題~
授業内容
中学3年生の数学「2つの連続した奇数の積に1を加えた数は4の倍数になる」ことを証明する。
困っていること
証明問題では無限にある数を文字を使って置き換えて表現する作業がまず基本となります。ここで躓く生徒が多いのが事実です。
今回の授業内容での指導では、
- 偶数と奇数を文字で表す方法を説明するだけで時間がかかってしまうこと
- 証明についてはあらかじめきまった型にはめて指導をすることになりがちなこと
この2点で困っておられました。
B先生に対する助言
— 1点目の文字での置き換えについて
中学2年生の数学でも文字を使った証明問題は扱います。そして、中学3年生でかけ算を用いたより発展的な証明問題が登場します。
数学は積み上げの教科です。これまでに学んだ内容との関連を示し、いきなり新しく出てきた学習内容だと生徒たちに思わせないようにすることが重要です。復習の内容を工夫すること、生徒に考えさせる部分と先生が教える部分を区別することが良いと助言されていました。
— 2点目の証明の型について
B先生はまず教科書に載っているような証明の型を教えてから、穴埋め問題等でそれにあてはめる形で具体的な証明問題を解いてもらうという指導をしていました。しかし、やり方を一緒に見ていきながら生徒たちにまず解かせてみて、不足している部分を授業で示してあげるのがよいのではないかという意見も出ていました。生徒の発想を取り入れながら、教科書にあるような型に近づけていくという発想からの提案でした。
まとめ
数学の先生は限られた時間の中で、その日の授業に関連する既習事項を復習させ、時には1年前に習ったことを生徒たちに思い出させ、授業をスムーズに展開させて新たなことを学ばせ理解させることが求められます。これは非常に高度なことであり、経験の浅い若手教員にとってはなかなか難しいことかもしれません。
今回は「教科書の型からの指導ではなく生徒たちの発想からの指導を」という、ある種演繹的な指導から帰納的な指導に変えてみるといった真逆の発想が出ていました。指導の際、時には立ち止まって自分の考えと異なる考えも取り入れてみることの必要性を感じました。
5 おわりに
本記事では、前半の2人の先生の模擬授業を通し、正負の数の減法と証明問題に関する指導上のノウハウや留意点をご紹介しました。いかがでしたでしょうか?
後編では、関数の導入と因数分解に関するベテラン教員の皆さんのご意見をご紹介いたします。
記事はこちら⇒「関数の導入(中1)・因数分解の指導法~伊丹市中学校数学科研修会での模擬授業を通して<後編>~」
(文責・編集 EDUPEDIA編集部 笠井真由・横山尚人)









コメント