分数（小学4年算数）同値分数で計算への種まきを！

本単元で身に付けたい資質・能力

本単元では、分母の異なる同値分数に注目することで、分母や分子が増えることによって生じる分数の大きさの変化を理解する能力を養う。また、数直線を使って分数を体系的に理解することの良さに気付き、今後の生活や学習に活用しようとする態度を育む。

単元の評価基準

• 知識・技能：同値分数を見つけることができる。
• 思考・判断・表現：同値分数であることを説明することができる。
• 主体的に取り組む態度：数直線や具体物、倍数の概念を用いて、同値分数を見つけようとする。

導入｜数直線で確認～異分母分数をものさしでイメージ～

前時までにやっておきたい種まき

分数の学習では「ものさし」という合言葉を用いて、通分を含めた和や差の計算に向けた種まきをすると良い。
ここで言う「ものさし」とは、縮尺を表す言葉だと理解してほしい。例えば、½と⅓では「（分子が）同じ1」だが「2つに分けたうちの1つ」と「3つに分けたうちの1つ」だから、異なる大きさの数である。この分母が異なる状態（単位分数が異なる状態）を「違うものさし」と表現している。

重要なのはイメージの共有と、違うものさしのままでは比較しにくいことへの理解である。

本時の目標は、違うものさしでも同じ大きさの数は確かに存在すると気付くことである。

通分とは、比較しにくい違うものさしの数を同じものさしで比較するための作業であり、「ものさし」という合言葉による一貫した指導のゴールとなる。

導入で驚きを！比較クイズ

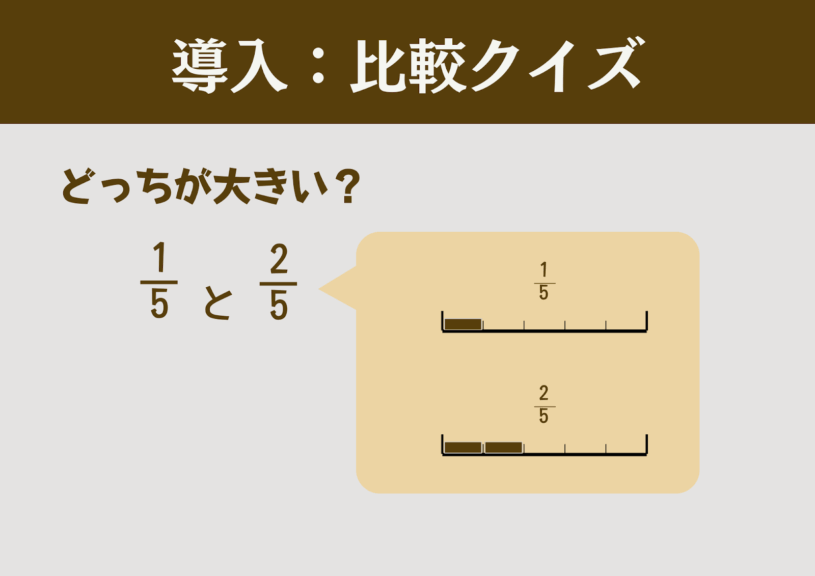
本時の導入では「分数の比較クイズ」を行う。
ルールは以下の通り。

1. 2つの分数を提示し、児童はどちらが大きいかを挙手で答える。
2. 児童は先の答えの根拠を、図やものさしを用いて説明する。

時短のため、ルール2については児童の理解度不足を感じたときのみの実施で良い。
真分数や仮分数、帯分数を交えると瞬時に答えられない児童も増えるので、ルール2が必要になるだろう。
クイズの最終問題には、同値分数（½と2/4等）を提示する。

等しい大きさであると分かったところで、どちらも所詮は「半分」であることを伝える。

細かい説明よりも分かりやすい「半分」という認識が、児童に大きな納得感と無数の同値分数の存在に気付くきっかけを与えてくれる。

展開｜同値分数を見つけるアクティブラーニング

ペアで学ぶ「半分を探せ！」

ここからはペア活動で同値分数への理解を深める。

ペア活動「半分を探せ！」のルール

• ペアで½の同値分数を探す。
• ½、2/4以外に3個見つけたら挙手をし、教員に回答する。

もちろん「半分」という言葉のおかげですぐに見つかるだろう。早く終わったペアには発見した同値分数の特徴について考えさせる。

ここで気付かせたいのは、以下の2点である。

• 分母が常に分子の2倍
• ½の同値分数は、½の分母、分子をそれぞれ等倍したもの

分母分子をそれぞれ等倍したものが同値分数であることについては、数直線よりもケーキ等を等分する考え方を用いて説明することでより理解が深まる。この際ケーキの総量を増やすのではなく、さらに細かく分割した図を用いて「ケーキの総量は変わらない」と意識づける説明が有効。

ペアで学ぶ「¼を探せ！」

続いてペア活動「¼を探せ！」を行う。ルールは先の活動と同様であり、数値が¼となるだけである。「半分」という考え方が直接的に使えない分クイズ自体に苦戦する児童も多少出るが、「半分のさらに半分」というヒントを出すことにより、½と大差ない考えでクリアできるだろう。
ここでも先と同様の気付きが得られるだろう。

• 分母が常に分子の4倍
• ½の同値分数は、½の分母、分子をそれぞれ等倍したもの

分数の値を一定に保つためには分母や分子がどのように変化すれば良いのかについて、気付いたことをノートにまとめ、数直線でのまとめに入る。

ペアで学ぶ番外編「¾を探せ！」

より難易度の高いペア活動を行いたい場合や、2つのペア活動を終えてなお時間を余らせているペアがいた場合には、ペア活動「¾を探せ！」を行うと良い。「分母が常に分子の4/3倍」となってしまい、分数の計算を習っていない段階ではとても難しく感じられるだろう。

この問題について、児童は以下のプロセスで乗り越えられる。

1. ¼の同値分数を発見する
2. ¾は、プロセス1の数を3つ集めた数（和）
   または、全体からプロセス1の数を除いた数（差）と回答する

和や差は計算上扱っていないが、数直線や図を用いて考えることはできるので、チャレンジ問題として秘めておくには良い問題だ。

まとめ｜数直線で異分母の分数の増え方をまとめよう

数直線でのまとめ～通分への布石～

最後に数直線を使って、これまでの学びを整理する。
上記画像の四角の枠を埋めながら同値分数を確認し、本時の振り返りを行う。
ここでは、以下の3点に重点を置くと良い。

• （同値分数を活用し、）ものさしを変えられること
• ペアワークで確認した点
• 分子が同じ数では、分母が大きいほど小さい分数になること

½＝3/6と⅓＝2/6を例にとり、「ものさしを変えると正確な比較ができること」には必ず触れておきたい。これが小学5年生で学ぶ「通分」への大きな布石となる。

今まで児童は、「違うものさしで表された数」の比較を感覚的にしか判断できなかった。しかし、同値分数を活用することで同じものさしに変えられるようになり、これらの数を根拠をもって比べられるようになったのだ。

この流れを見越し、小学3年生で分数を学ぶ際には「同じものさしなら比べやすい」という意識をつけさせておくことを勧める。

執筆者

まき先生

中学高校で数学を教えている。体系的に教えるためには算数から学びなおす必要があると感じ、算数の授業案についても学習をすすめている。
実践的かつつながりを意識した授業案の作成に努める。