後々までの重要な計算
たし算やひき算をするとき、数を合成・分解する能力があるのとないのではずいぶん計算にかかる時間が違ってきます。4年生、5年生と学年が上がるにしたがって複雑な筆算を学習することになります。筆算をするときに計算を億劫に感じる子供は基本的な計算力が身に付いていません。サクランボ算、つまり数をいかに分解するかを考える計算は、足し算をするにあたっても、引き算をするにあたっても基本的な計算になると思います。
・
関連記事として、下記↓リンクをご参照ください。
小学校1年生のためのくりさげ・くりあげの定着方法 (岡篤先生)
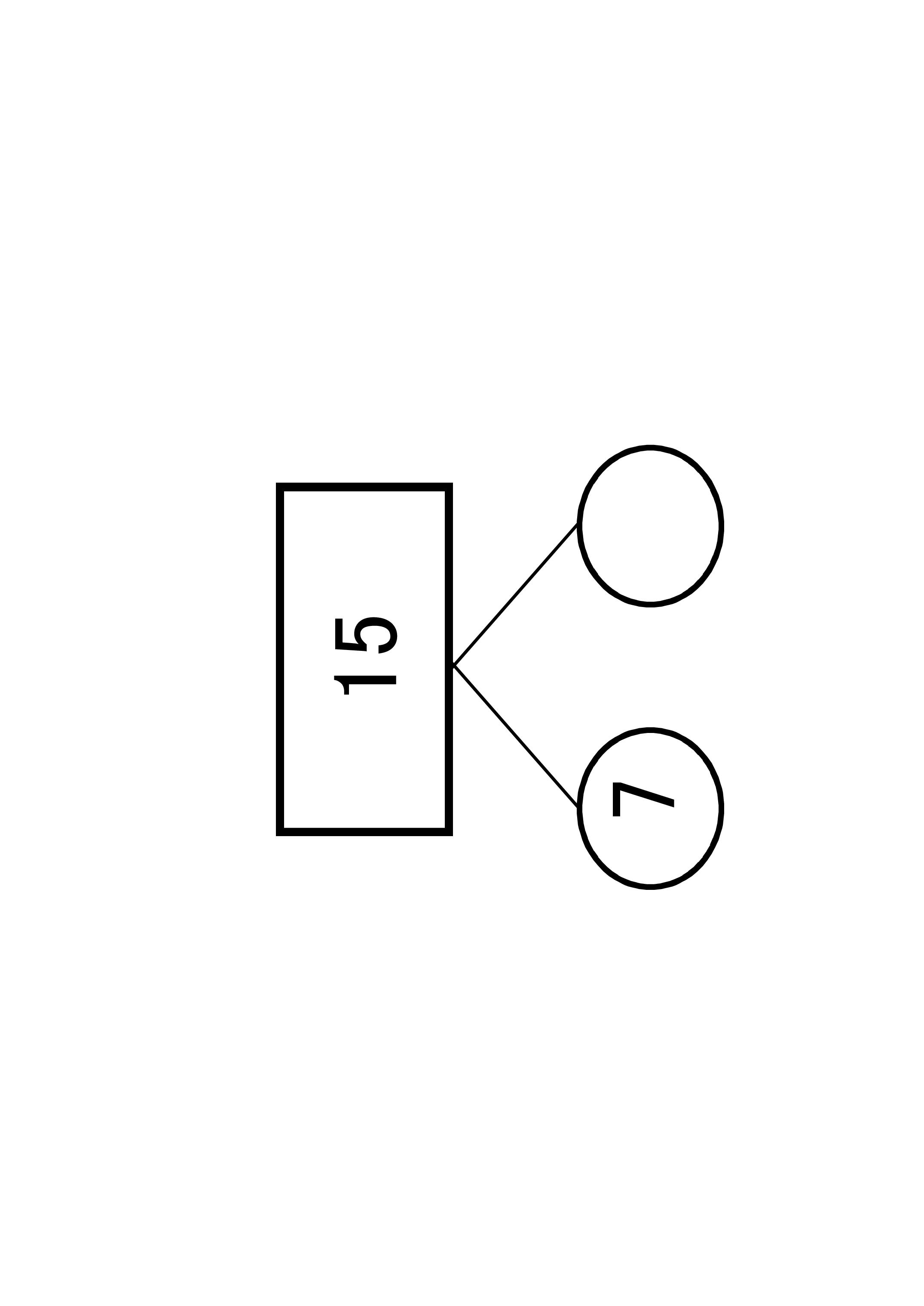
例えば・・・
8+6を計算するとき、10を8と2、6を2と4に瞬時に分解することができれば、計算はぐんとスピードアップします。13−7を計算するときは、13が4と9・5と8・6と7に分解(繰り上がりパターン)できることを覚えていれば、即座に答えを出すことができます。
サクランボ算となる10までの数の分解は45個あり、11から18までの数の分解は36個あります。これらをあわせても、たった81個のパターンしかありません。
「12=8+4」と「12=4+8」を同一と考えれば、10までの数の分解は25個あり、11から18までの数の分解は20個です。これらをあわせても、たった45個のパターンしかありません。
繰り返しサクランボ算を練習することにより、すぐに数を分解できるようにしておけば、計算はとても楽になると思います。特に10の分解は計算をするにあたって繰り返し要求されるものなので、1と9・2と8・3と7・4と6・5と5というパターンをしっかり身につけておけば、計算全体が楽になります。
サクランボ算の全パターンが練習できるエクセルファイルを添付↓しましたので、是非、繰り返して子供にやらせてみてください。
・
さくらんぼ算 全パターン.xlsx
サクランボ算10まで.zip
サクランボ算11から18.zip
基本に戻って補習を
実際にやってみると、高学年になってもこのプリント1枚をするのに3分以上かかってしまう子供がいます。そういった子供を取り出して、放課後の補充学習等で少なくとも3分以内にできるように鍛えてあげてください。目途は3分以内、できれば2分以内です。計算の速い子供は1分以内でできてしまいます。九九のように覚えてしまっているのです。このプリントに取り組むときには、毎回必ずデータをとってください。何分何秒でできるようになったのか、子供が自分の成長を見て取ることができれば、伸び方も違ってくると思います。
1・2年生ではできなかったことも、高学年になればできるようになるかもしれません。あきらめずに基本に戻って何度も繰り返し学習すれば、5年生での複雑な筆算の問題(小数÷小数!)を解く場面で大きな助けになると思います。









コメント