サンドウィッチ
・
かけ算の文章問題を解くとき、「かける数」と、「かけられる数」を分からせるのには少々時間がかかります。反対にしても答えが同じなのだから、どっちでもいいように思えてしまうので、余計に間違えやすいのかもしれません。という課題について、その2です。
・
九九は「かけられる数」になる物(事)が増えているため、答えは当然「かけられる数」になる物(事)と同じ物(事)となるわけです。具体的に言うと、「みかん」をかければ答えも「みかん」、「タコの足」をかければ答えも「タコの足」、「長さ」をかければ答えも「長さ」なのです。
・
みかんが4個ずつ3枚のお皿に盛ってあります。みかんは何個あるでしょう。
という問題であれば、必ず「答」はかならずみかんなわけですから、「かけられる数」もみかんになります。つまり、立式した時に単位も書くと、「4個×3枚=12個」になります。つまり、「かけられる数」を「答」の単位は同じになるということです。
私は個人的には「被乗数」と「乗数」の順番なんてどうでもいいように考えていますが、教科書がそう教えるように誘導しています。文科省が発行している↓の「【算数編】小学校学習指導要領(平成29年告示)解説 (PDF:6MB)」でも、P115に「言い換えると,(一つ分の大きさ)×(幾つ分)=(幾つ分かに当たる大きさ)と捉えることができる。」書いています。
20211102-mxt_kyoiku02-100002607_04.pdf (mext.go.jp)
教科書も指導要領解説も、ややあいまいさを残した表現で説明しています。そうなると、かけ算の順序は被乗数と積の単位が同じになるように教えざるを得ないのが現状です。なので上記の
みかんが4個ずつ3枚のお皿に盛ってあります。みかんは何個あるでしょう。
の式が「3×4」でも構わないのかどうかを現場で議論してみても答えは出ません。そんな大人の事情を踏まえああだこうだ教えても2年生の子供には分かりません。
そこで、こんなふうに言います。
・
「かけ算は、後ろと前で、単位がいっしょです。サンドイッチになるように書いてください。」
で、3×4などと間違っている子供には、みかんであれば、
・
「答はみかんが何個だよね。『個個でサンド』になっていますか。」
と、問い直してあげます。
・
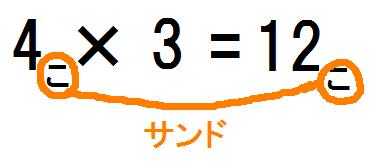
・
カエルであれば、「『匹匹でサンド』になっていますか。」です。長さであれば「『メートルメートルでサンド』になっていますか。」です。お金であれば、「『円円でサンド』になっていますか。」です。
・
子供たちが慣れるまでは、立式したときに必ず単位を書くようにさせるのもいいと思います。
邪道かもしれませんが
イージーな教え方かもしれません。もしかすると、算数研究専門家の関係者の方々からすると邪道と言われるかもしれませんが、イメージができない子供にとってはこの方法で確実に楽に立式ができると思います。何らかの助けにはなるかな、と思います。
—————-
割り算で包含所の時だけ単位のサンドイッチにならないので、あくまでかけ算では単位のサンドイッチです。
とにかく、「教師・親・ドリル等・塾等」で主張が違っていて、教科書が「かける数とかけられる数の立式のルール」の明言を避けているため、混乱しています。ので、被害者となる学力が低い子供にはすっきり理解できる形をとってあげたいです。
※ この記事をアップしてかなり時間が経っています。かけ算の「乗数・被乗数」に関する議論がネット上でもかなり話題になりました。興味のある方は、「かけ算 順序」等で検索してみて下さい。
筆者としては、小学校で上記のように教えておけば、後々、「あー、先生がサンドイッチとか言っていたけど、いろんな考え方もあるんだ」と思い起こすきっかけになればという程度に考えています。教育現場にあまりパーフェクトな正しさを求めて仕方ないのではないかと思うのですが・・・
関連記事
九九の暗唱が苦手な子供をサポートするプリント ~ゆっくり楽に確実に【教材】
九九暗唱の鍛え方・九九の聞き方 ~全員が九九を言えるように









コメント
コメント一覧 (14件)
まったく意味のない指導である。
掛け算はどちらも順序でもかまわない。
「反対にしても答えが同じなのだから、どっちでもいいように思えてしまうので、余計に間違えやすいのかもしれません。」
ではなく、どちらでもいいのであって、「一方のみが正しい」というのが間違い。
掛け算の順序が必要だとする論者はしばしば
「 数学では掛け算の順序はどうでも良いが、算数では順序が必要である 」
と主張するようです。
しかし実際には、小学校の範囲内でも高学年の授業では、2年生に教えたはず
のルールに違反するやりかたが行われています。
例えば、この edupedia にも記事を出したことのある先生の授業です。
http://www.h4.dion.ne.jp/~amajima/matsuisenshu.pdf
「1万円札を 100枚 かさねたら、高さ(厚さ)が1cmになった。
1万円札を 254100枚 かさねたら、高さはどれだけか?」
という問題の解き方を
□ = 254100 × 1 ÷ 100 = 2541cm
としています。
254100 の単位(?) は「枚」ですから、ここでは「単位のサンドイッチ」が守ら
れていません。
この先生おひとりだけが間違えているということではなく、比の単元では、掛け算
の順序が守られていない例が、多数みられます。
上の学年ではどうでも良くなるルールを2年生に身につけさせるのは、全くの無駄
であると考えます。
2年生の息子がよく理解してなかったので、
私がかけられる数を説明しても理解できずにいましたが、これは分かりやすいと思います。
上記のコメントを読んで、確かにって思うところもありますが、2年生の段階でしっかり理解できていないと割り算が入った時も躓きそうで。
テストでかけられる数とかける数が逆に書いて×をもらってきても、なぜ違うのか理解できていませんでした。
今の授業では教えるではなくて、簡単に説明しかしないので家庭学習においてはこの説明はありがたい。
私は当年とって50歳に近い者なのですが、情けない事に、ごく最近までこの掛ける数と掛けられる数のルールを知らなかったのです。
単位系を揃えるために、答えの単位を掛けられる数として式の前に置く。ごく初歩的なこんなルールも理解していないままこの年まで来てしまいました。去年くらいに盛んになった、例の「6×8を8×6と書いてはいけない」騒動で、このルールを知り、ハッと目覚めさせていただいたのです。
件の騒動では、逆に数式を書いたくらいでバツになるのは馬鹿げてる、教師の傲慢、交換法則により正しいはい論破、なる、私より遥かに高学歴で社会的地位も高そうな人士が得意満面で書き込みしています。
何ということか。何故彼らはその後の学習の進捗でつまづかなかったのか。不思議でならないです。
このコメント欄ですら得意げに書き込んでる始末。しかし、単位系統一を徹底するには、最初は分数の計算式の形で書かないと理解不能になると思いました。日本の算数授業はこの言葉故の欠点がある気がします。
ちゃんとバツを付けてくれる今の授業に、子供達は感謝することでしょうね。
「みかんが4個ずつ3枚のお皿に盛ってあります。みかんは何個あるでしょう。」について、単位(?)付きで式を書いた時の、単位そのものが間違っていることに気づいていないために生じた混乱でしょう。
4個ずつ皿に盛ってある、ですから、4(個)ではなく、4(個/皿)とであるという話をしているわけですよね。それが3(皿)あるのですから、みかん全部は
4(個/皿)×3(皿)=12(個)
となります。これを逆にしたとしても、
3(皿)×4(個/皿)=12(個)
です。
みかん2個が乗った皿が1枚あって、そこに同じように2個乗った皿を追加して、全部でみかんはいくつ?というのを足し算で出す場合を考えます。単位が(個/皿)のままで足すと最後が(個)にならないように思えるかもしれません。しかしよくよく考えると、皿が1枚、と勘定した時点で、
2(個/皿)×1(皿)
の計算を暗黙のうちに行っていることになります。すると、足し算の前に行われる暗黙の単位換算を含め
2(個/皿)×1(皿)+2(個/皿)×1(皿)=4(個)
と正しい結果を得ることになります。
本来なら、3個「ずつ」乗った皿、という記載に忠実に単位の方を(個/皿)としなければいけないのに、ただの(個)で済ませてしまったことが、後々日本語の文章に引きずられてかけ算の順序によって単位が合わないという事態を引き起こしているだけではないですか。
「単位系を揃えるために、答えの単位を掛けられる数として式の前に置く。ごく初歩的なこんなルール」なるものは存在しません。
掛け算を「1つ分×いくつ分」で導入する。導入でこうしているというだけのことで順序に深い意味はない。仮に「1つ分×いくつ分」に拘っても、「4人に3個ずつ」なら「3個の塊が4つだから3×4」ということになるが、各自に1個ずつ配るのを3回繰り返すなら4個が3回分で4×3となるわけで、3×4、4×3、どちらでも構わない。
ところが算数教育では「3×4が正しくて4×3が間違い」とされる。
で、この「正しい順序」にするための方法が「答えの単位・助数詞と同じものを最初におく」というもの。
「掛け算の順序が大切」という算数教育界の人の意見に「どちらでもいいとすると問題文の意味を考えなくなる」というのがあるが、この「サンドイッチ」は「考えなくても教師が想定する順序に出来る方法」であり、このようなものが提唱されること自体が、順序指導の無意味さを物語っている。
さらにこれを「ルール」と思ってしまうのは、便宜的な暗記法を本当のことだと思っているわけで、1582年本能寺の変を「イチゴパンツで本能寺」とすると覚えやすいというのを、「明智光秀はイチゴパンツを愛用していた」と思ってしまうようなものである。
もし本当にこのようなサンドイッチルールがあるなら、縦3m横4mの長方形の面積は、3m×4m=12m となってしまう。
またこのような手法は、問題文そのものを理解しないで単位・助数詞にだけ着目して式を立てる癖を誘発しかねず、百害あって一利なしと言わざるを得ない。
「何故彼らはその後の学習の進捗でつまづかなかったのか。不思議でならないです。」という疑問もあるようだが、そもそも掛け算の順序はどっちでもいいのだから、掛け算の順序はどっちでもいいと正しく理解しているわけでつまずく必然性がない。
むしろ、1つ分×いくつ分の順序に拘る人が、高校数学でやる順列組み合わせでつまずかないのが不思議だった。ABCDの並べ替えは、4×3×2×1と式を立てる人が多いが、「4人に3個ずつなら3×4の順序のみが等しい」という立場からしたら、1×2×3×4としないとならないはず。
これに関しては、彼らは順列を求める式を、小学校算数の掛け算の概念の延長ではなく、公式として覚えているだけなので、自ら課したルールに反しているという認識がないことが判明した。
いずれにしても、掛け算の順序に拘るなど有害無益だし、この本文にあるような単位のサンドイッチなど百害あって一利なしである。
4個が3つで12というのは、算数で線分図で理解しやすくするためではないでしょうか。
答えとしては同じ12だけれど線分図でいう
4+4+4であって3+3+3+3ではない
かける数とかけられる数という概念は数学には無い。しかし、その昔数学とともに歩んできた物理には似て非なる概念、単位というものがある。みかんの問題は物理学的視点と、いうか初歩の単位の視点でみると4個/皿のお皿を何皿という問題になる。
つまり4個/皿X3皿=12個(皿という単位がが計算の結果消えるのに注目)
または3皿X4個/皿=12個と、矛盾なく12個という単位で表記される
この3は3皿という立派な単位のある数であり、ただの数字ではない。
ここで割り算のわからない小学校2年生に、/皿なんていう単位がわかるはずがないという事実がある。
それはその通り。だから、単位系を小学校に持ち込むことはできない。割り算だけならともかく、m^2と2乗(平方)まであるので、単位を教える事はできない
だからといって、かけられる数、かける数等、のちの概念に矛盾する概念を教えるのはおかしいという事をいいたい。当初は単位について教えられないが、なんとか概念だけでもと思い無理やり作った概念かとおもう。確かに教えなければならないとなれば、他にいい方法もないだろう。しかし、そもそも何故むりやり間違った概念を教えるのか?ということになる。上の問題で、3は数字ではなく(かける数ではなく)皿という単位をもった値である。中学の時に少し習う。単位という概念を持ったときに、いきなりわけがわからなくなる。物理量等意味があるものは、全て単位がある。ところが上記の教育をうけた結果、かける数という誤った概念に縛られ、単位を無視した掛け算、つまりは下記の問題等で平気で数字をかけたりするということがある
時速10m/時で動く芋虫が1分間に移動する距離は何mか?
これは昔は小学5,6年生の問題だが、これを数学でおちこぼれた中学生が
10mx1=10m
と答えてしまう。
勿論本当は10m/時÷60分/時x1分=10m/時x(1/60)時/分x1分
=1/6m
ときっちりmとなって答えがでる
このように、単位を抑えるのが数学を実用の世界と結びつける事になり重要な項目で、これを理解しないと、中学高校で大変苦労する事になる。
しかし、かける数という単位もへったくれもない数字を持ち出す事が、この単位を学んだ後の混乱を生むのだ。
3つ子の魂100までもというが、誤った概念を子供に教えるべきではない。単位を教えられない時期については、そういうものとして単位をあとからつける(そこに何故?ときかれたら、おおきくなったらわかる。今は難しいといえばいい)という昔からの教育で十分だとおもう。現在のこの方針は、とてもいいものとは思えない
難しいことを言ってらっしゃるかた、こちらはいかがでしょうか。
今まで色々と読んでいて、私は一番納得しました。
https://www.vissenburg.com/2018/05/25/あすなろ199%E3%80%80かけられる数xかける数/
数学教師です。算数て難しいですね。
絶対教えられません。
「こんなことをくどくど言っても2年生の子供には分かりません。そこで、こんなふうに言います」
って、これは酷いのではないかしら。いくつも誤認があるようです。
まず、理解させてあげるのが教員の仕事でしょう。
次に、こんなことをくどくど言っても2年生の子どもにはわからない、という観察は当たっているかもしれませんが、理解できない原因を「子どもだから」と決めつけていますが、本当の原因は「こんなことをくどくどというような説明の仕方が下手だから」でしょう。
子どもの認知・理解力や成長過程について理解が浅く、説明自体もうまくないということなので、算数教育にかかわらないほうが良いのではないかと思います。
こんなのを真に受ける人がいたとしたらかわいそうです。
anonさん、コメント、ありがとうございます。
小学(2年)生算数における「乗数・被乗数」に関する議論はかなり昔から答えが出ないまま続いています。けっこう喧々諤々の議論になることが多く、この記事のコメント欄だけでもけっこう読みごたえがあるご意見が寄せられています。
「『乗数・被乗数』の順序を教えるなど、ナンセンスである」といった内容のご意見がけっこう数学畑の専門家の方々に多いというのが私の体感です。学習指導要領も教科書も教科書会社もルールをにおわせながらも、明確には示していないのが実情ではないかと思います。
どうやって教えればよいのか、採点時にはどうすればいいのか、現場には定まった答えがなく、混乱しています。もし、この議論についてのanonさんのお考えがありましたら、是非、お教えいただけると幸いです。
因みに、
学習指導要領では、以下のように書かれているだけです。
—————————————–
ア 次のような知識及び技能を身に付けること。
(ア) 乗法の意味について理解し,それが用いられる場合について知る
こと。
(イ) 乗法が用いられる場面を式に表したり,式を読み取ったりするこ
と。
(ウ) 乗法に関して成り立つ簡単な性質について理解すること。
(エ) 乗法九九について知り,1位数と1位数との乗法の計算が確実に
できること。
(オ) 簡単な場合について,2位数と1位数との乗法の計算の仕方を知
ること。
—————————————–
また、学習指導要領解説(算数)では、乗数・被乗数の順序について下記のアドレスで示してはいますが、なんだか曖昧です。あくまで例示を説明するにとどまり、乗数・被乗数の順序についての明確な(学術的な)ルールがあるとは書かれていません。引用が長くなりますので、下記アドレスP113あたりから読んでみられると、よいかと思います。
—————————————–
https://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2019/03/18/1387017_004.pdf
(@_@)
別の方も答えられているが、個、皿、人はすべて単位です。
それなのに個だけを単位とするから子供たちが混乱するのではないでしょうか?
apjさんが書かれているように、単位も式に入れてあげると個しか残らなくなります。
ただ、個/皿は割り算であり、小学校3年生で習うのでこの時点ではできません。
ですので、すくなくとも小学校2年生の時はどちらでも正解。
3年生以降も単位をしっかり理解していれば、正解として良いと思います。