100までの数で、素数はいくつあるか
25個です。
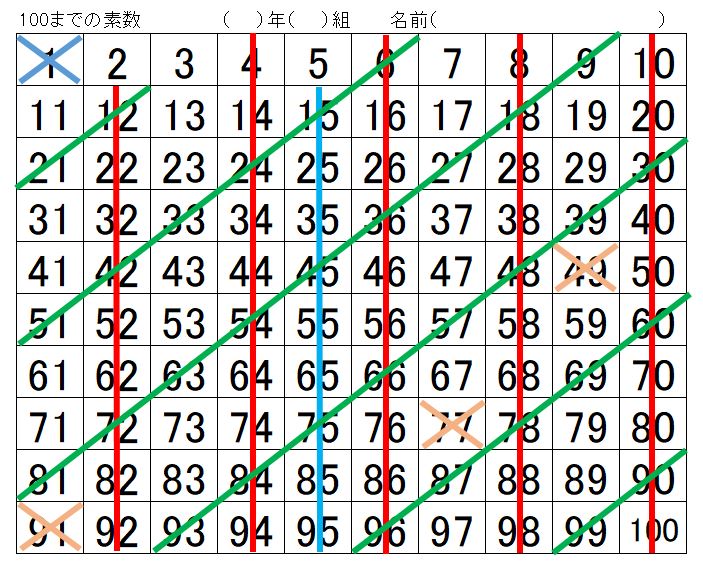
素数プリントを作りました↓ので、ご利用ください。
約数の学習をする時に、素数について知識を持っていると便利ですね。例えば「51」の約数を考えるとき、素数と思っていると「1,51」となりますが、素数でないことが分かっていれば、「1,3,17,51」と、正解を出すことができます。
小学校のスタンダード問題ではそれほど難しい約数の問題が出ることはないとは思いますが、とりあえず、100までの素数は約数の学習をする時に、覚えておくと便利ですね。
約数に関しては、
等をご参照ください。
素数かどうかを判断するコツ
50までは、素数かどうか分かりやすいですが、「51」あたりから怪しくなってきます。
(0)まず、10までの素数を確認します。→→→ 1は素数でない、2・3・5・7は素数。
その後、プリントで素数ではないものを消していきます。
(1)偶数は「2」を除いて素数ではない
(2)1の位が5であると、「5」を除いて素数ではない。
(3)3の倍数は「3」を除いて素数ではなく、表中ではななめに表れる。(線を引いて消させてみてください。)
(4)1の位が0であると、素数ではない。(そもそも偶数で(1)に当てはまっている)
(5)九九の答えは素数ではない。((1)~(4)を実行すると49だけが九九の答えで残っています)
これで、残りが絞れてきます。
絞った残りの中で77,91は素数ではありません。
77=11×7
はすぐ頭に思い浮かびますので、消せると思います。
あとは、
91=13×7
これが分かりにくいですね。
上の説明をもう少し短く言うと、
①2・3・5の倍数は素数ではない。(ただし、2・3・5は素数)
②1は素数ではない。(これは、よく分からなくなりますので要注意)
③49・77・91は素数ではない。(どれも7の倍数です。49=7×7、77=7×11、91=7×13)
ですね。
※表を使わなかった場合、51,57,87,91あたりが、素数かどうか迷う(ひっかかる)ところではないでしょうか。
各桁の数の合計が3の倍数なので、3で割ることができることが分かります。
51=17×3 →→→ 5+1=6
57=19×3 →→→ 5+7=12
87=29×3 →→→ 8+7=15
となると、
91=13×7
これさえ覚えていれば、100までの素数は攻略ですね。









コメント